题目内容
已知函数f（x）=x2+ax-2b．若a，b都是区间[0，4]内的数，则使f（1）＞0成立的概率是（ ）A．
B．
C．
D．
【答案】分析：本题利用几何概型求解即可．在a-o-b坐标系中，画出f（1）＞0对应 的区域，和a、b都是在区间[0，4]内表示的区域，计算它们的比值即得．
解答：
解：f（1）=1+a-2b＞0，即a-2b+1＞0，
则a，b都是从区间[0，4]任取的一个数，有f（1）＞0，
即满足条件：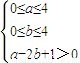
转化为几何概率如图所示，
其中A（0，
），C（4，
），
事件“f（1）＞0”的表示的平面区域为阴影部分，
其面积为s=
（OA+BC）×OB=
（
+
）×4=6，
∴事件“f（1）＞0”的概率为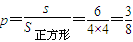
．
故选C．
点评：本小题主要考查几何概型、二次函数的性质等基础知识．古典概型和几何概型是我们学习的两大概型，古典概型要求能够列举出所有事件和发生事件的个数，而不能列举的就是几何概型，几何概型的概率的值是通过长度、面积、和体积的比值得到．
解答：
解：f（1）=1+a-2b＞0，即a-2b+1＞0，则a，b都是从区间[0，4]任取的一个数，有f（1）＞0，
即满足条件：
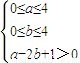
转化为几何概率如图所示，
其中A（0，
），C（4，），事件“f（1）＞0”的表示的平面区域为阴影部分，
其面积为s=
（OA+BC）×OB=（+）×4=6，∴事件“f（1）＞0”的概率为
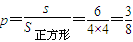．故选C．
点评：本小题主要考查几何概型、二次函数的性质等基础知识．古典概型和几何概型是我们学习的两大概型，古典概型要求能够列举出所有事件和发生事件的个数，而不能列举的就是几何概型，几何概型的概率的值是通过长度、面积、和体积的比值得到．
练习册系列答案
快捷英语周周练系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|