Question

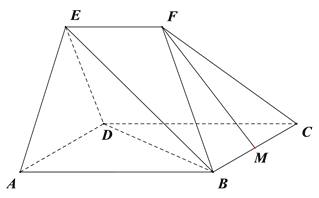
【题目】如图1，在正方形中，点分别是的中点，与交于点，点分别在线段上，且．将分别沿折起，使点重合于点，如图2所示.

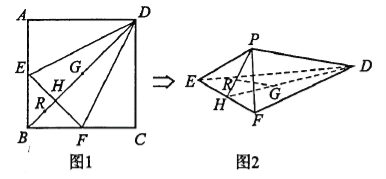
（1）求证：平面；

（2）若正方形的边长为4，求三棱锥的内切球的半径.

Answer 1

【答案】（1）详见解析；（2）.

【解析】

试题分析：（1）因为点重合于点（该点记为），由原图可知，三条直线两两垂直，那么平面,又根据图中给的比例关系，可知,根据平行关系可知,平行线与同一平面垂直，即证明；(2)因为内切球的球心到三棱锥的四个面的距离相等，所以可将三棱锥的体积分为四个小三棱锥的体积和，而每一个小三棱锥的高就是内切球的半径，这样根据体积和可求得内切球的半径.

试题解析：（1）在正方形中，为直角，

∴在三棱锥中，三条线段两两垂直．．．．．．．．．．．．．．．．．．．2分

∴平面．．．．．．．．．．．．．．．．．．．．．．．．．．．3分

∵，即，∴在中，．．．．．．．．．．．．．．．4分

∴平面．．．．．．．．．．．．．．．．．．．．6分

（2）正方形边长为4．

由题意，．．．．．．．．．．．．．．．．．．．7分

∴．

．．．．．．．．．．．．．．．．．．10分

设三棱锥内切球半径为．

则三棱锥的体积

∴．

∴三棱锥的内切球的半径为．．．．．．．．．．．．．．．．．．．．．12分