题目内容
【题目】已知椭圆 
，斜率为 
的动直线l与椭圆C交于不同的两点A，B．
（1）设M为弦AB的中点，求动点M的轨迹方程；
（2）设F1 ， F2为椭圆C在左、右焦点，P是椭圆在第一象限上一点，满足 
，求△PAB面积的最大值．
【答案】
（1）解：设M（x，y），A（x1，y1），B（x2，y2），
由 
①， 
②；
①﹣②得： 
， 
，即 
．
又由中点在椭圆内部得 
，
∴M点的轨迹方程为 ， ；
（2）解：由椭圆的方程可知：F1（﹣ 
，0）F2（ ，0），P（x，y）（x＞0，y＞0）， 
=（﹣ ﹣x，﹣y）， 
=（ ﹣x，﹣y），
由 =（﹣ ﹣x，﹣y）（ ﹣x，﹣y）=x2﹣3+y2=﹣ 
，即x2+y2= 
，
由 
，解得：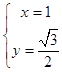 
，则P点坐标为 
，…
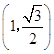设直线l的方程为 
，
，整理得： 
，由△＞0得﹣2＜m＜2，
则 
， 
，…
， 
，
∴ 
．…
，
当且仅当m2=4﹣m2，即 
时，取等号，
∴△PAB面积的最大值1．
【解析】（1）由由 
①， 
②；①﹣②得： 
， 
，即 
，由M在椭圆内部，则 
，即可求得动点M的轨迹方程；（2）由向量数量积的坐标运算，求得P点坐标，求得直线l的方程，代入椭圆方程，利用韦达定理，点到直线的距离公式及三角形的面积公式，根据基本不等式的性质，即可求得△PAB面积的最大值．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
