题目内容
(本题12分)
设数列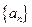 的前
的前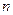 项和为
项和为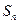 ,已知
,已知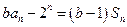 .
.
(1)证明:当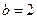 时,
时,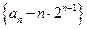 是等比数列;
是等比数列;
(2)求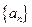 的通项公式
的通项公式
设数列
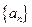 的前
的前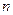 项和为
项和为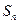 ,已知
,已知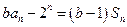 .
.(1)证明:当
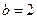 时,
时,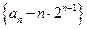 是等比数列;
是等比数列;(2)求
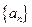 的通项公式
的通项公式解:由题意知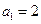 ,且
,且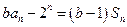 ,
,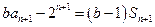
两式相减得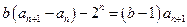 ,即
,即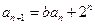 ①
①
(1)当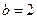 时,由①知
时,由①知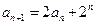
于是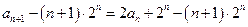
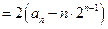
又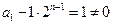 ,所以
,所以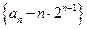 是首项为1,公比为2的等比数列。----(6分)
是首项为1,公比为2的等比数列。----(6分)
(2)当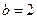 时,由(1)知
时,由(1)知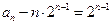 ,即
,即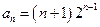
当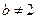 时,由①得
时,由①得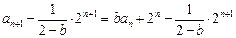
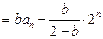
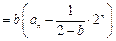
因此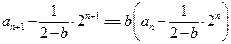
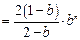
得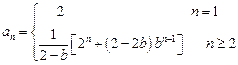 --------------(12分)
--------------(12分)
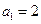 ,且
,且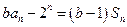 ,
,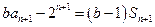
两式相减得
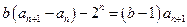 ,即
,即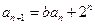 ①
①(1)当
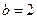 时,由①知
时,由①知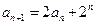
于是
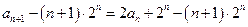
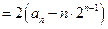
又
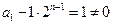 ,所以
,所以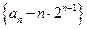 是首项为1,公比为2的等比数列。----(6分)
是首项为1,公比为2的等比数列。----(6分)(2)当
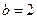 时,由(1)知
时,由(1)知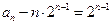 ,即
,即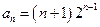
当
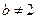 时,由①得
时,由①得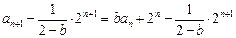
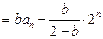
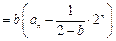
因此
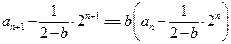
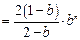
得
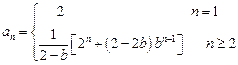 --------------(12分)
--------------(12分)略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
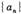 是公比大于1的等比数列,
是公比大于1的等比数列,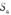 为数列
为数列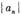 的前n项和,已知
的前n项和,已知 ,且
,且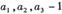 成等差数列.
成等差数列.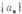 的通项公式
的通项公式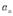 ;
;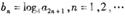 ,求和:
,求和: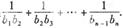
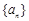 的前n项和为
的前n项和为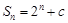 ,其中c为常数,则该数列
,其中c为常数,则该数列



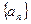 的通项公式是
的通项公式是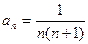 ,若前n项和为
,若前n项和为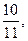 则
则 _____
_____ 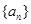 的前
的前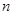 项和
项和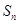 满足:
满足: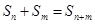 ,且
,且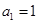 ,那么
,那么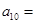 ( )
( )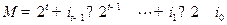 ,其中
,其中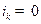 或
或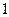 (
(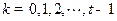 ,
,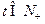 ),并记
),并记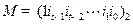 ,对于给定的
,对于给定的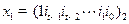 ,构造数列
,构造数列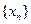 如下:
如下: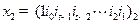
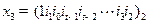 ,
,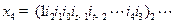 ,若
,若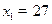 ,则
,则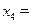 (用
(用 数字作答).
数字作答). .解答题
.解答题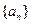 的前n项和
的前n项和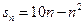 ,求数列
,求数列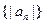
 的前n项和。
的前n项和。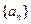 中,如果存在非零的常数
中,如果存在非零的常数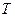 ,使得
,使得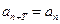 对于任意正整数
对于任意正整数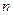 均成立,那么就称数列
均成立,那么就称数列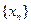 满足
满足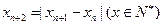 ,若
,若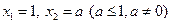 ,当数列
,当数列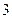 时,则数列
时,则数列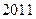 项的和
项的和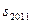 为( )
为( )



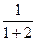 ,
,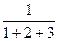 ,…的前n项和S
,…的前n项和S