题目内容
在△ABC中,B(10,0),直线BC与圆Γ:x2+(y-5)2=25相切,切点为线段BC的中点.若△ABC的重心恰好为圆Γ的圆心,则点A的坐标为 .
(0,15) 或 (-8,-1)
解析试题分析:设BC的中点为D,设点A(x1,y1)、C(x2,y2),则由题意可得ΓD⊥BC,且D(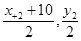 ).故有圆心Γ(0,5)到直线AB的距离ΓD=r=5.
).故有圆心Γ(0,5)到直线AB的距离ΓD=r=5.
设BC的方程为y-0=k(x-10),即 kx-y-10k=0.则有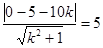 ,解得 k=0或 k=-
,解得 k=0或 k=-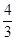 .
.
当k=0时,有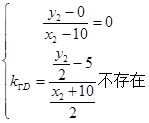 ,当
,当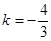 时,有
时,有 ,
,
解得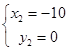 ,或
,或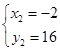 .再有三角形的重心公式可得
.再有三角形的重心公式可得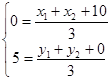 ,由此可得
,由此可得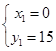 或
或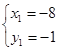
故点A的坐标为(0,15)或(-8,-1),
故答案为(0,15)或(-8,-1).
考点:直线与圆的位置关系.
点评:本题主要考查直线和圆的位置关系的应用,点到直线的距离公式、斜率公式、三角形的重心公式,属于中档题.

练习册系列答案
相关题目
 ,AB=3,则切线AD的长为___ _____.
,AB=3,则切线AD的长为___ _____.
 的点数共有______ 个。
的点数共有______ 个。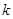 为何实数,直线
为何实数,直线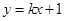 与曲线
与曲线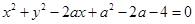 恒有交点,则实数
恒有交点,则实数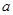 的取值范围为 。
的取值范围为 。 关于
关于 轴对称的圆的方程为______________.
轴对称的圆的方程为______________. 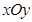 中,“直线
中,“直线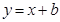 ,
,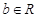 与曲线
与曲线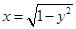 相切”的充要条件是 .
相切”的充要条件是 .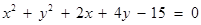 上到直线
上到直线 的距离为
的距离为 的点的个数是 _ .
的点的个数是 _ .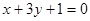 和圆
和圆 相交于点A、B,则AB的垂直平分线方程是
相交于点A、B,则AB的垂直平分线方程是