题目内容
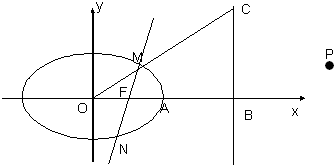 (2012•烟台三模)已知椭圆
(2012•烟台三模)已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
| b |
| a |
| OB |
| OA |
| OA |
| OC |
| a2 |
| c |
(1)求椭圆的方程;
(2)求证:N、B、P三点共线;
(3)求△BMN的面积.的最大值.
分析:(1)根据
=2
,
•
=8,可得
=2a且
=8,从而可求椭圆方程;
(2)设直线l:y=k(x-1),与椭圆方程联立
,利用韦达定理,同时确定
,
的坐标,证明
,
共线,即可证得结论;
(3)求出d为B到l的距离d=
,弦长|MN|=
,即可表示出面积,从而可求△BMN的面积的最大值.
| OB |
| OA |
| OA |
| OC |
| a2 |
| c |
| a3 |
| c |
(2)设直线l:y=k(x-1),与椭圆方程联立
|
| BP |
| BN |
| BP |
| BN |
(3)求出d为B到l的距离d=
| 3|k| | ||
|
| 1+k2 |
| (x1+x2)-4x1x2 |
解答:(1)解:因为
=2
,
•
=8,所以
=2a且
=8,所以a=2,c=1
所以b=
=
,所以椭圆方程为:
+
=1…(4分)
(2)证明:设直线l:y=k(x-1),M(x1,y1),N(x2,y2)
则由
,消去y得(3+4k2)x-8k2x+4k2-12=0,
所以x1+x2=
,x1x2=
…(6分)
由于P(8-x1,y1),
=(4-x1,y1),
=(x2-4,y2),
因为(4-x1)y2-(x2-4)y1=4(y1+y2)-x1y2-y1x2=4k(x1+x2-2)-2kx1x2+k(x1+x2)=4k(
-2)-2k
+k
=0…(8分)
当l⊥x轴时,也满足
故
,
共线,所以N、B、P三点共线…(9分)
(3)解:记d为B到l的距离,则d=
,|MN|=
,…(10分)
所以S=
d|MN|=
|k|
=
<
…(12分)
当l⊥x轴时,S=
,…(13分)
所以△BMN的面积的最大值为
…(14分)
| OB |
| OA |
| OA |
| OC |
| a2 |
| c |
| a3 |
| c |
所以b=
| a2-c2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
(2)证明:设直线l:y=k(x-1),M(x1,y1),N(x2,y2)
则由
|
所以x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
由于P(8-x1,y1),
| BP |
| BN |
因为(4-x1)y2-(x2-4)y1=4(y1+y2)-x1y2-y1x2=4k(x1+x2-2)-2kx1x2+k(x1+x2)=4k(
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
| 8k2 |
| 3+4k2 |
当l⊥x轴时,也满足
故
| BP |
| BN |
(3)解:记d为B到l的距离,则d=
| 3|k| | ||
|
| 1+k2 |
| (x1+x2)-4x1x2 |
所以S=
| 1 |
| 2 |
| 3 |
| 2 |
(
|
| 9 |
| 2 |
1-
|
| 9 |
| 2 |
当l⊥x轴时,S=
| 9 |
| 2 |
所以△BMN的面积的最大值为
| 9 |
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三点共线,考查三角形面积的计算,解题的关键是直线与椭圆方程的联立,利用韦达定理解题.

练习册系列答案
相关题目