题目内容
在锐角 中,
中,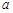 、
、 、
、 分别为角
分别为角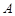 、
、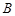 、
、 所对的边,且
所对的边,且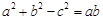 .
.
(1)求角 的大小;
的大小;
(2)若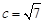 ,且
,且 的面积为
的面积为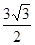 ,求
,求 的值.
的值.
(1) 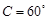 ;(2)
;(2) 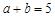 .
.
解析试题分析:(1)利用角C的余弦定理推论,即可求出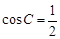 ,进而求出角
,进而求出角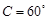 ;(2)由于
;(2)由于 的面积为
的面积为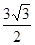 和(1)中
和(1)中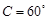 ,根据面积
,根据面积 可求得
可求得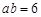 ,再利用边C的余弦定理,可得
,再利用边C的余弦定理,可得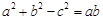 ,对式中
,对式中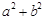 用
用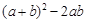 替换化简,将
替换化简,将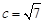 代入,即可求出
代入,即可求出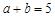 .
.
(1) ,
,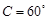 . .5分
. .5分
(2)由 ,得
,得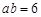 . .8分
. .8分
又由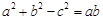 ,且
,且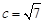 ,得
,得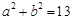 . .11分
. .11分
所以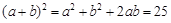 ,从而
,从而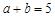 . .13分.
. .13分.
考点:1.解三角形;2.余弦定理及其推论;3.三角形面积公式.

练习册系列答案
相关题目
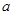 ,
, ,
, ,且
,且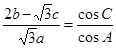 .
. 的值;
的值;  ,
,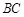 边上的中线
边上的中线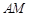 =
= ,求
,求 的面积.
的面积. 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知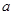 =3,
=3, =
=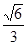 ,
,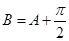 ,
,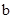 得值;
得值;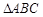 中,角
中,角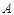 ,
, ,
,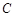 所对的边分别是
所对的边分别是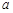 ,
,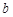 ,
,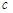 ,已知
,已知 ,
,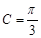 .
.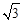 ,求
,求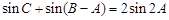 ,求
,求 .
.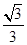 ,求sinA的值;
,求sinA的值; 中,
中,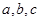 分别为角
分别为角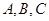 所对的边,且
所对的边,且
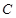 的大小;
的大小; 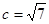 ,且
,且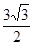 ,求
,求 的值.
的值.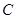 、
、 是两个小区所在地,
是两个小区所在地,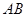 的垂直距离分别为
的垂直距离分别为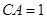
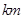 ,
,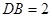
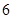
 ,在
,在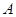 、
、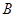 、
、 ,在
,在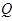 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得
 )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
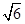 ,∠B=2∠A,
,∠B=2∠A,