题目内容
已知二次函数 .
.
(1)若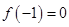 ,试判断函数
,试判断函数 零点个数;
零点个数;
(2)是否存在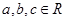 ,使
,使 同时满足以下条件
同时满足以下条件
①对任意 ,且
,且 ;
;
②对任意 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(3)若对任意 且
且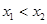 ,
, ,试证明存在
,试证明存在 ,
,
使 成立。
成立。
(1)函数 有两个零点。(2)当
有两个零点。(2)当 时,
时, 同时满足条件①、②. (3)利用零点存在性定理证明即可
同时满足条件①、②. (3)利用零点存在性定理证明即可
解析试题分析:(1)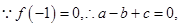
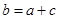
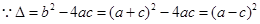 当
当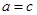 时
时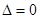 ,
,
函数 有一个零点; 3分
有一个零点; 3分
当 时,
时,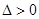 ,函数
,函数 有两个零点。 5分
有两个零点。 5分
(2)假设 存在,由①知抛物线的对称轴为x=-1,
存在,由①知抛物线的对称轴为x=-1,
∴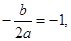 即
即 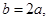 7分
7分
由②知对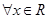 ,都有
,都有
令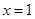 得
得
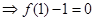
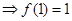
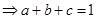 又因为
又因为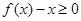 恒成立,
恒成立,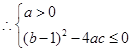
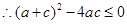 ,即
,即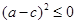 ,即
,即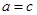
由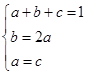 得
得 , 10分
, 10分
当 时,
时,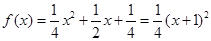 ,
,
其顶点为(-1,0)满足条件①,又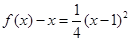
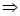 对
对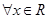 ,
,
都有 ,满足条件②.
,满足条件②.
∴存在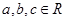 ,使
,使 同时满足条件①、②. .12分
同时满足条件①、②. .12分
(3)令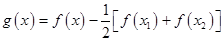 ,则
,则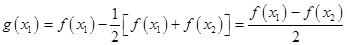
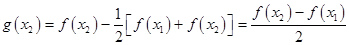 ,
,
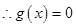 在
在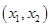 内必有一个实根。即
内必有一个实根。即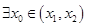 ,
,
使 成立 18分
成立 18分
考点:本题考查了函数的零点及恒成立问题
点评:①二次函数、一元二次方程和一元二次不等式是一个有机的整体,也是高考热点,要深刻理解它们相互之间的关系,能用函数思想来研究方程和不等式,便是抓住了关键.②二次函数 的图像形状、对称轴、顶点坐标、开口方向等是处理二次函数问题的重要依据.
的图像形状、对称轴、顶点坐标、开口方向等是处理二次函数问题的重要依据.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
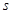 平方米,矩形一边的长为
平方米,矩形一边的长为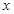 米(如图所示)
米(如图所示)
 的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后
的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后 到达现场开始救火,已知消防队在现场每人每分钟平均可灭火
到达现场开始救火,已知消防队在现场每人每分钟平均可灭火 ,所消耗的灭火材料、劳务津贴等费用每人每分钟
,所消耗的灭火材料、劳务津贴等费用每人每分钟 元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人
元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人 元,而每烧毁
元,而每烧毁 森林的损失费为
森林的损失费为 元,设消防队派了
元,设消防队派了 名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时
名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时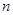
 .
.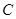 (单位:万元)与日产量
(单位:万元)与日产量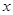 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式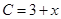 ,每日的销售额
,每日的销售额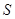 (单位:万元)与日产量
(单位:万元)与日产量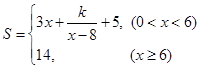
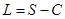 ,且当
,且当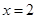 时,
时,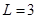 .
.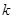 的值;
的值;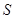 平方米.
平方米.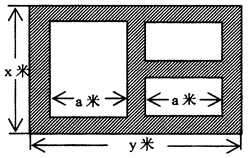
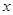 表示
表示 和用
和用


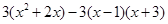
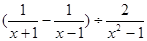
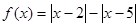 .
.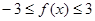 ;
;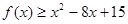 的解集.
的解集.