题目内容
【题目】已知椭圆![]() ,过点
,过点![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)若点![]() 平分线段
平分线段![]() ,试求直线
,试求直线![]() 的方程;
的方程;
(2)设与满足(1)中条件的直线![]() 平行的直线与椭圆交于
平行的直线与椭圆交于![]() 两点,
两点,![]() 与椭圆交于点
与椭圆交于点![]() ,
,![]() 与椭圆交于点
与椭圆交于点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)设![]() ,代入椭圆方程,两式相减可求得直线
,代入椭圆方程,两式相减可求得直线![]() 的斜率,从而得直线方程;(2)设
的斜率,从而得直线方程;(2)设![]() ,同时设
,同时设![]() ,下面只要证得
,下面只要证得![]() 即可,为此由
即可,为此由![]() 得
得![]() ,并把
,并把![]() 坐标代入椭圆方程,变形得
坐标代入椭圆方程,变形得![]() ,即
,即![]() ,同理有
,同理有![]() , 这两式相减,并由
, 这两式相减,并由![]() 可证得结论.
可证得结论.
试题解析:(1)设![]() ,则
,则![]() ,①
,①![]() ,②
,②
①-②得![]() ,
,
即![]() ,
,
又![]() ,∴
,∴![]() ,
,
故直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
(2)设![]() ,且
,且![]() ,
,
则有![]() ,即
,即![]() ,
,
将点![]() 的坐标分别代入椭圆方程:
的坐标分别代入椭圆方程:
![]() ,①
,①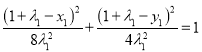 ,②
,②
②![]() -①得
-①得![]() ,
,
易知![]() ,故约去
,故约去![]() 得
得![]() ,③.
,③.
同理有![]() ,④
,④
由④-③得![]() ,
,
由已知![]() 斜率为
斜率为![]() ,有
,有![]() ,
,
得![]() ,即
,即![]() ,即
,即![]() ,所以
,所以![]()

练习册系列答案
相关题目