题目内容
【题目】已知函数f(x)是定义在R上的奇函数，并且当x∈(0，＋∞)时，f(x)＝2x.
(1)求f(log2
)的值；
(2)求f(x)的解析式．
【答案】(1)－3. (2) f(x)＝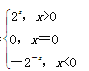
.
【解析】
试题(1)因为f(x)为奇函数，且当x∈(0，＋∞)时，f(x)＝2x，
所以f(log2
)＝f(－log23)＝－f(log23)＝－2log23＝－3. (6分)
(2)设任意的x∈(－∞，0)，则－x∈(0，＋∞)，
因为当x∈(0，＋∞)时，f(x)＝2x，所以f(－x)＝2－x，
又因为f(x)是定义在R上的奇函数，则f(－x)＝－f(x)，
所以f(x)＝－f(－x)＝－2－x，即当x∈(－∞，0)时，f(x)＝－2－x； （8分)
又因为f(0)＝－f(0)，所以f(0)＝0， (10分)
综上可知，f(x)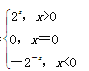＝. (12分)
练习册系列答案
相关题目
