题目内容
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 为矩形,
为矩形, ![]() 为
为![]() 中点,
中点, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,则
,则![]() 为
为![]() 的中点,由
的中点,由![]() 为
为![]() 中点,利用三角形中位线定理可得
中点,利用三角形中位线定理可得![]() ,从而根据线面平行的判定定理可得
,从而根据线面平行的判定定理可得![]() 平面
平面![]() ;(Ⅱ)由勾股定理可得
;(Ⅱ)由勾股定理可得![]() ,根据线面垂直的性质定理得
,根据线面垂直的性质定理得![]() 平面
平面![]() ,故
,故![]() ,再根据线面垂直的判定定理可得
,再根据线面垂直的判定定理可得![]() 平面
平面![]() ,故
,故![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角,在直角
所成的角,在直角![]() 中可得
中可得![]() .
.
试题解析:
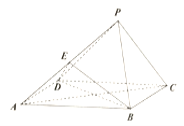
(Ⅰ)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() .
.
因为![]() 为矩形,所以
为矩形,所以![]() 为
为![]() 的中点.
的中点.
在![]() 中,由已知
中,由已知![]() 为
为![]() 中点,所以
中点,所以![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)在![]() 中,
中, ![]() ,
, ![]() ,
,
所以![]() ,
,
即![]() .
.
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() .
.
又因为![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
故![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角.
所成的角.
在直角![]() 中
中![]() ,
, ![]() ,
,
所以![]() .
.
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、直线和平面成的角的定义及求法,属于难题. 证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.

【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|