题目内容
设直线l1与l2的方程分别为a1x+b1y+c1=0与a2x+b2y+c2=0,则“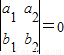 ”是“l1∥l2”的( )
”是“l1∥l2”的( )A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】分析:若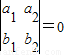 ,则a1b2-a2b1=0,若a1c2-a2c1=0,则l1不平行于l2;若“l1∥l2”,则a1b2-a2b1=0,所以
,则a1b2-a2b1=0,若a1c2-a2c1=0,则l1不平行于l2;若“l1∥l2”,则a1b2-a2b1=0,所以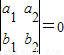 ,故可得结论
,故可得结论
解答:解:若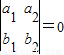 ,则a1b2-a2b1=0,若a1c2-a2c1=0,则l1不平行于l2,故“
,则a1b2-a2b1=0,若a1c2-a2c1=0,则l1不平行于l2,故“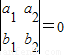 ”是“l1∥l2”的不充分条件;
”是“l1∥l2”的不充分条件;
若“l1∥l2”,则a1b2-a2b1=0,∴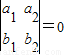 ,故“
,故“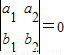 ”是“l1∥l2”的必要条件
”是“l1∥l2”的必要条件
所以“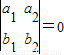 ”是“l1∥l2”的必要而不充分条件
”是“l1∥l2”的必要而不充分条件
故选B.
点评:本题重点考查四种条件的判定,解题的关键是理解行列式的定义,掌握两条直线平行的条件.
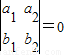 ,则a1b2-a2b1=0,若a1c2-a2c1=0,则l1不平行于l2;若“l1∥l2”,则a1b2-a2b1=0,所以
,则a1b2-a2b1=0,若a1c2-a2c1=0,则l1不平行于l2;若“l1∥l2”,则a1b2-a2b1=0,所以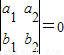 ,故可得结论
,故可得结论解答:解:若
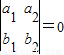 ,则a1b2-a2b1=0,若a1c2-a2c1=0,则l1不平行于l2,故“
,则a1b2-a2b1=0,若a1c2-a2c1=0,则l1不平行于l2,故“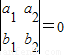 ”是“l1∥l2”的不充分条件;
”是“l1∥l2”的不充分条件;若“l1∥l2”,则a1b2-a2b1=0,∴
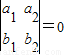 ,故“
,故“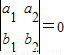 ”是“l1∥l2”的必要条件
”是“l1∥l2”的必要条件所以“
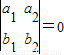 ”是“l1∥l2”的必要而不充分条件
”是“l1∥l2”的必要而不充分条件故选B.
点评:本题重点考查四种条件的判定,解题的关键是理解行列式的定义,掌握两条直线平行的条件.

练习册系列答案
相关题目
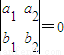 ”是“l1∥l2”的( )
”是“l1∥l2”的( )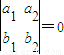 ”是“l1∥l2”的( )
”是“l1∥l2”的( )