题目内容
设直线l1与l2的方程分别为a1x+b1y+c1=0与a2x+b2y+c2=0,则“a1b2-a2b1=0”是“l1∥l2”的( )
分析:两条直线平行时,一定可以得到a1b2-a2b1=0成立,反过来不一定成立,由此确定两者之间的关系.
解答:解:若a1b2-a2b1=0,不妨设a1=0,b1=1,a2=0,b2=1,c1=c2,此时两直线重合,所以不充分.
若l1∥l2,则必有a1b2-a2b1=0成立.
所以“a1b2-a2b1=0”是“l1∥l2”的必要不充分条件.
故选B.
若l1∥l2,则必有a1b2-a2b1=0成立.
所以“a1b2-a2b1=0”是“l1∥l2”的必要不充分条件.
故选B.
点评:本题考查充分条件和必要条件的判断,要求掌握判断充分条件和必要条件的方法:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
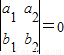 ”是“l1∥l2”的( )
”是“l1∥l2”的( )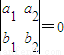 ”是“l1∥l2”的( )
”是“l1∥l2”的( )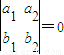 ”是“l1∥l2”的( )
”是“l1∥l2”的( )