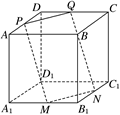
题目内容
在正方形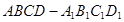 中,
中,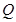 是
是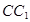 的中点,
的中点,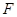 是侧面
是侧面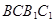 内的动点且
内的动点且 //平面
//平面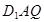 ,则
,则 与平面
与平面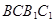 所成角的正切值得取值范围为 .
所成角的正切值得取值范围为 .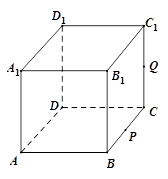
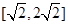
解析试题分析:设平面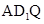 与直线BC交于点G,连接AG、QG,则G为BC的中点
与直线BC交于点G,连接AG、QG,则G为BC的中点
分别取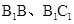 的中点M、N,连接
的中点M、N,连接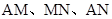 ,则
,则
∵
∴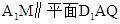 .同理可得
.同理可得 ,
,
∵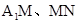 是平面
是平面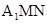 内的相交直线
内的相交直线
∴平面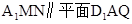 ,
,
由此结合 ,可得直线
,可得直线 ,即点F是线段
,即点F是线段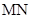 上上的动点.
上上的动点.
设直线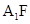 与平面
与平面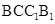 所成角为
所成角为 ,
,
运动点F并加以观察,可得:当F与M(或N)重合时,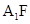 与平面
与平面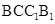 所成角等于
所成角等于 ,此时所成角
,此时所成角 达到最小值,满足
达到最小值,满足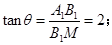 当F与MN中点重合时,
当F与MN中点重合时,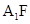 与平面
与平面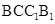 所成角达到最大值,满足
所成角达到最大值,满足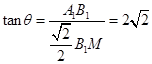 ,
,
∴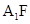 与平面
与平面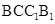 所成角的正切取值范围为
所成角的正切取值范围为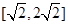 ,
,
故答案为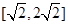 .
.
考点:正方体的结构特征,直线与平面所成角,空间面面平行与线面平行关系的判定.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
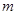 ,
,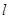 和平面
和平面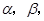 且
且 ,给出下列四个命题:
,给出下列四个命题: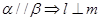 ②
②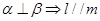 ③
③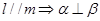 ④
④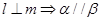
 中,
中,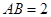 ,点
,点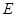 为
为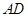 的中点,点
的中点,点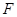 在
在 上,若
上,若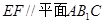 ,则线段
,则线段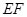 的长度等于______.
的长度等于______.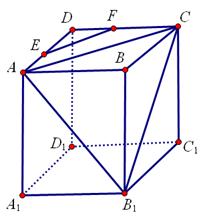
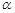 ,
,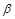 ,
, 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题: 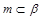 ,
,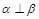 ,则
,则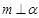 ;
;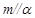 ,
,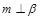 ,则
,则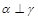 ,则
,则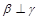 ;
;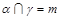 ,
,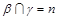 ,
,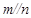 ,则
,则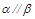 .
. 、
、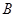 为正方体的两个顶点,
为正方体的两个顶点, 、
、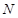 、
、 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出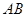 //平面
//平面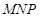 的图形的序号是 .
的图形的序号是 .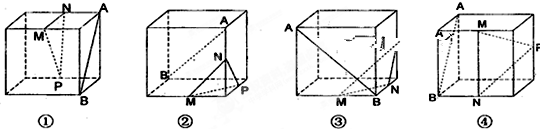
 绕直线
绕直线 向上转动
向上转动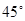 到
到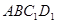 ,再将所得正方形
,再将所得正方形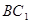 向上转动
向上转动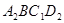 ,则平面
,则平面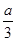 ,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.