题目内容
给出下列命题:①若α、β是第一象限的角且α<β,则tanα<tanβ;
②存在实数α,使sinαcosα=1;
③y=sin(
| 5π |
| 2 |
④存在实数α,使sinα+cosα=
| 3 |
| 2 |
⑤x=
| π |
| 8 |
| 5π |
| 4 |
其中正确命题的序号是
分析:令α=60°,β=30°+360°,可得①不正确.
由于sin2α+cos2α=1,故sinαcosα=1 不可能,得②不正确.
y=sin(
-x)=cosx,是偶函数,故③正确.
若sinα+cosα=
,平方可得sin2α=
>1,矛盾,故④不正确.
当x=
时,函数y=sin(2x+
)=-1,故x=
是函数的一条对称轴方程,故⑤正确.
由于sin2α+cos2α=1,故sinαcosα=1 不可能,得②不正确.
y=sin(
| 5π |
| 2 |
若sinα+cosα=
| 3 |
| 2 |
| 5 |
| 4 |
当x=
| π |
| 8 |
| 5π |
| 4 |
| π |
| 8 |
解答:解:①不正确,如α=60°,β=30°+360°,α<β,但不满足tanα<tanβ.
②不正确,由于sin2α+cos2α=1,故sinαcosα=1 不可能.
③正确,∵y=sin(
-x)=sin(
-x)=cosx,是偶函数.
④不正确,若sinα+cosα=
,则有1+sin2α=
,sin2α=
>1,矛盾.
⑤正确,当x=
时,函数y=sin(2x+
)=sin
=-1,函数取得最小值,故x=
是函数的一条对称轴方程.
故答案为:③⑤.
②不正确,由于sin2α+cos2α=1,故sinαcosα=1 不可能.
③正确,∵y=sin(
| 5π |
| 2 |
| π |
| 2 |
④不正确,若sinα+cosα=
| 3 |
| 2 |
| 9 |
| 4 |
| 5 |
| 4 |
⑤正确,当x=
| π |
| 8 |
| 5π |
| 4 |
| 3π |
| 2 |
| π |
| 8 |
故答案为:③⑤.
点评:本题考查正弦函数的对称性,奇偶性和值域,熟练掌握正弦函数的图象性质是解题的关键.

练习册系列答案
相关题目
 、
、 ,两个不同平面
,两个不同平面 、
、 ,给出下列命题:
,给出下列命题:
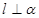 ,则
,则 则
则 在平面
在平面 。
。 ,对任意
,对任意 ,运算“
,运算“ ”具有如下性质:
”具有如下性质: ; (2)
; (2) ; (3)
; (3) .
. :
: ,则
,则 ;
; ,且
,且 ,则a = 0;
,则a = 0; ,且
,且 ,
, ,则a = c.
,则a = c. 和
和 为不重合的两个平面,给出下列命题:1若
为不重合的两个平面,给出下列命题:1若 与
与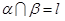 ,若
,若 ;4直线
;4直线 的充要条件是
的充要条件是 、
、 ,且m⊥
,且m⊥ ,
,