题目内容
在平面直角坐标系中,已知向量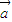 =(-1,2),又点A(8,0),B(n,t),C(ksinθ,t)
=(-1,2),又点A(8,0),B(n,t),C(ksinθ,t)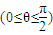 .
.(1)若
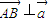 ,且
,且 为坐标原点),求向量
为坐标原点),求向量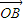 ;
;(2)若向量
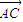 与向量
与向量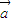 共线,当k>4,且tsinθ取最大值4时,求
共线,当k>4,且tsinθ取最大值4时,求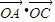 .
.
【答案】分析:(1)根据所给的点的坐标写出向量的坐标,根据两个向量垂直数量积为零,得到一个关于变量的方程,题目另一个条件是两个向量模长之间的关系,列出方程解出结果.
(2)根据向量共线的充要条件,写出变量之间的关系式,根据二次函数的最值特点得到结果,求出变量的值写出向量的数量积.
解答:解:(1)∵点A(8,0),B(n,t),
∴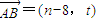 ,
,
∵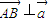 ,
,
∴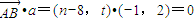 ,
,
得n=2t+8.
则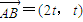 ,又
,又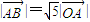 ,
,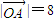 .
.
∴(2t)2+t2=5×64,
解得t=±8,
当t=8时,n=24;当t=-8时,n=-8.
∴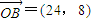 或
或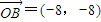 .
.
(2)∵向量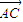 与向量
与向量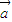 共线,
共线,
∴t=-2ksinθ+16,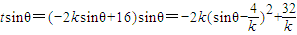 .
.
∵k>4,
∴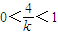 ,
,
故当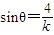 时,tsinθ取最大值
时,tsinθ取最大值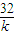 ,有
,有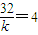 ,得k=8.
,得k=8.
这时,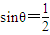 ,k=8,tsinθ=4,得t=8,则
,k=8,tsinθ=4,得t=8,则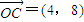 .
.
∴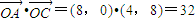 .
.
点评:要让学生体会思路的形成过程,体会数学思想方法的应用.要学生发现解题方法和思路的形成过程,总结解题规律.学生要搞好解题后的反思,从而提高学生综合应用知识分析和解决问题的能力.
(2)根据向量共线的充要条件,写出变量之间的关系式,根据二次函数的最值特点得到结果,求出变量的值写出向量的数量积.
解答:解:(1)∵点A(8,0),B(n,t),
∴
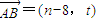 ,
,∵
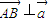 ,
,∴
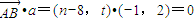 ,
,得n=2t+8.
则
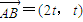 ,又
,又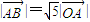 ,
,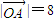 .
.∴(2t)2+t2=5×64,
解得t=±8,
当t=8时,n=24;当t=-8时,n=-8.
∴
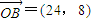 或
或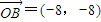 .
.(2)∵向量
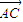 与向量
与向量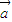 共线,
共线,∴t=-2ksinθ+16,
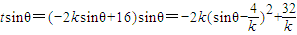 .
.∵k>4,
∴
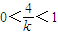 ,
,故当
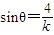 时,tsinθ取最大值
时,tsinθ取最大值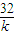 ,有
,有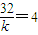 ,得k=8.
,得k=8.这时,
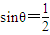 ,k=8,tsinθ=4,得t=8,则
,k=8,tsinθ=4,得t=8,则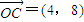 .
.∴
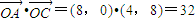 .
.点评:要让学生体会思路的形成过程,体会数学思想方法的应用.要学生发现解题方法和思路的形成过程,总结解题规律.学生要搞好解题后的反思,从而提高学生综合应用知识分析和解决问题的能力.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目