题目内容
已知椭圆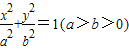 的左焦点为
的左焦点为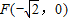 ,点F到右顶点的距离为
,点F到右顶点的距离为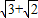
(I)求椭圆的方程;
(II)设直线l与椭圆交于A、B两点,且与圆
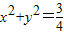 相切,求△AOB的面积为
相切,求△AOB的面积为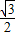 时求直线l的斜率.
时求直线l的斜率.
【答案】分析:(I)利用椭圆的左焦点为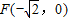 ,点F到右顶点的距离为
,点F到右顶点的距离为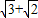 ,求出椭圆的几何量,即可求得椭圆的方程;
,求出椭圆的几何量,即可求得椭圆的方程;
(II)当直线l的斜率不存在时,不符合题意;当直线l的斜率存在时,设l的方程,利用直线l与圆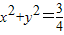 相切,确定m,k的关系,再利用韦达定理及△AOB的面积为
相切,确定m,k的关系,再利用韦达定理及△AOB的面积为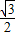 ,即可求得直线l的斜率.
,即可求得直线l的斜率.
解答:解:(I)由题意得c=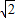 ,a+c=
,a+c=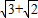
∴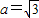 ,∴b2=a2-c2=1
,∴b2=a2-c2=1
∴椭圆的方程为 ;
;
(II)当直线l的斜率不存在时,l的方程为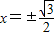 ,代入椭圆方程,可得
,代入椭圆方程,可得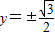 ,此时|AB|=
,此时|AB|=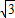 ,△AOB的面积为S=
,△AOB的面积为S=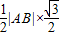 =
= ,不符合题意;
,不符合题意;
当直线l的斜率存在时,设l的方程为y=kx+m,A(x1,y1),B(x2,y2),
∵直线l与圆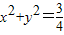 相切,∴
相切,∴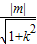 =
=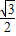 ,即
,即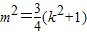
直线与椭圆方程联立,消去y可得(3k2+1)x2+6kmx+3m2-3=0
∴x1+x2=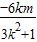 ,x1x2=
,x1x2=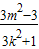
∴|AB|=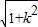 ×
×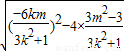 =
=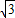 ×
×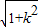
∴ ×
×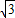 ×
×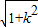 ×
×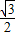 =
=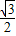 ,∴k=±
,∴k=±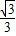
即直线l的斜率为±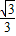 .
.
点评:本题考查椭圆的标准方程,考查直线与圆、椭圆的位置关系,考查三角形面积的计算,正确运用韦达定理是关键.
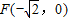 ,点F到右顶点的距离为
,点F到右顶点的距离为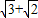 ,求出椭圆的几何量,即可求得椭圆的方程;
,求出椭圆的几何量,即可求得椭圆的方程;(II)当直线l的斜率不存在时,不符合题意;当直线l的斜率存在时,设l的方程,利用直线l与圆
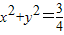 相切,确定m,k的关系,再利用韦达定理及△AOB的面积为
相切,确定m,k的关系,再利用韦达定理及△AOB的面积为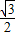 ,即可求得直线l的斜率.
,即可求得直线l的斜率.解答:解:(I)由题意得c=
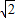 ,a+c=
,a+c=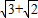
∴
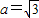 ,∴b2=a2-c2=1
,∴b2=a2-c2=1∴椭圆的方程为
 ;
;(II)当直线l的斜率不存在时,l的方程为
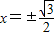 ,代入椭圆方程,可得
,代入椭圆方程,可得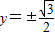 ,此时|AB|=
,此时|AB|=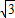 ,△AOB的面积为S=
,△AOB的面积为S=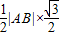 =
= ,不符合题意;
,不符合题意;当直线l的斜率存在时,设l的方程为y=kx+m,A(x1,y1),B(x2,y2),
∵直线l与圆
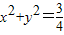 相切,∴
相切,∴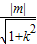 =
=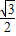 ,即
,即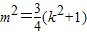
直线与椭圆方程联立,消去y可得(3k2+1)x2+6kmx+3m2-3=0
∴x1+x2=
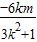 ,x1x2=
,x1x2=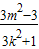
∴|AB|=
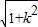 ×
×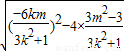 =
=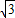 ×
×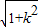
∴
 ×
×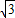 ×
×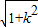 ×
×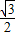 =
=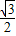 ,∴k=±
,∴k=±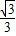
即直线l的斜率为±
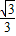 .
.点评:本题考查椭圆的标准方程,考查直线与圆、椭圆的位置关系,考查三角形面积的计算,正确运用韦达定理是关键.

练习册系列答案
相关题目
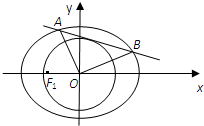 已知椭圆C:
已知椭圆C: 中,已知椭圆
中,已知椭圆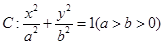 的左焦点为
的左焦点为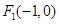 ,且椭圆
,且椭圆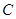 的离心率
的离心率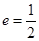 .
.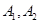 ,
,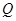 是椭圆
是椭圆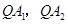 分别交
分别交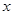 轴于点
轴于点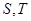 ,证明:
,证明: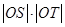 为定值,并求出该定值;
为定值,并求出该定值;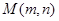 ,使得直线
,使得直线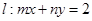 与圆
与圆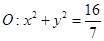 相交于不同的两点
相交于不同的两点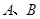 ,且
,且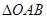 的面积最大?若存在,求出点
的面积最大?若存在,求出点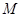 的坐标及对应的
的坐标及对应的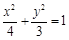 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
 ,求直线AB的斜率;
,求直线AB的斜率;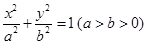 的左焦点为
的左焦点为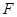
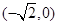 ,离心率e=
,离心率e=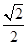 ,M、N是椭圆上的动
,M、N是椭圆上的动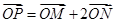 ,直线OM与ON的斜率之积为
,直线OM与ON的斜率之积为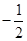 ,问:是否存在定点
,问:是否存在定点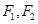 ,
,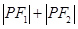 为定值?,若存在,求出
为定值?,若存在,求出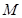 在第一象限,且点
在第一象限,且点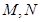 关于原点对称,点
关于原点对称,点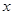 轴上的射影为
轴上的射影为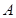 ,连接
,连接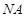 并延长
并延长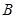 ,证明:
,证明: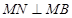 ;
; 的左焦点为
的左焦点为 ,右顶点为
,右顶点为 ,点
,点 在椭圆上,且
在椭圆上,且 轴, 直线
轴, 直线 交
交 轴于点
轴于点 .若
.若 ,则椭圆的离心率是( )w.w.w.七彩教育网.c.o.m
,则椭圆的离心率是( )w.w.w.七彩教育网.c.o.m  B.
B. C.
C. D.
D.