题目内容
函数f(x)=|x-1||2-x|
(1)作出函数f(x)的图象;
(2)方程f(x)=k(k∈R)中,k为何值时方程无解,2解,3解,4解?
(1)作出函数f(x)的图象;
(2)方程f(x)=k(k∈R)中,k为何值时方程无解,2解,3解,4解?
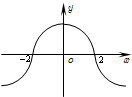
(1)函数f(x)=|x-1||2-x|=|(x-1)(x-2)|,如图所示:
(2)①若方程f(x)=k(k∈R)无解,则函数f(x)的图象和直线y=k没有交点,
数形结合可得 k<0,即当k<0时,方程f(x)=k(k∈R)无解.
②若方程f(x)=k(k∈R)有2个解,则函数f(x)的图象和直线y=k有2个交点,
数形结合可得 k>
,或k=0,即当k>
,或k=0时,方程f(x)=k(k∈R)有2个解.
③若方程f(x)=k(k∈R)有3个解,则函数f(x)的图象和直线y=k有3个交点,
数形结合可得 k=
,即当k=
时,方程f(x)=k(k∈R)有3个解.
若方程f(x)=k(k∈R)由4个解,则函数f(x)的图象和直线y=k有4个交点,
数形结合可得 0<k<
,即当 0<k<
时,方程f(x)=k(k∈R)有4个解.

(2)①若方程f(x)=k(k∈R)无解,则函数f(x)的图象和直线y=k没有交点,
数形结合可得 k<0,即当k<0时,方程f(x)=k(k∈R)无解.
②若方程f(x)=k(k∈R)有2个解,则函数f(x)的图象和直线y=k有2个交点,
数形结合可得 k>
| 1 |
| 4 |
| 1 |
| 4 |
③若方程f(x)=k(k∈R)有3个解,则函数f(x)的图象和直线y=k有3个交点,
数形结合可得 k=
| 1 |
| 4 |
| 1 |
| 4 |
若方程f(x)=k(k∈R)由4个解,则函数f(x)的图象和直线y=k有4个交点,
数形结合可得 0<k<
| 1 |
| 4 |
| 1 |
| 4 |


练习册系列答案
相关题目
 ,给出下列命题:
,给出下列命题: ②
② ;③y=f(x)图象关于(0,c)对称;④f(x)=0至多有两个实根。上述命题中,所有正确的序号是
;③y=f(x)图象关于(0,c)对称;④f(x)=0至多有两个实根。上述命题中,所有正确的序号是 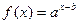 的图象如图,其中a、b为常数,则下列结论正确的是( )
的图象如图,其中a、b为常数,则下列结论正确的是( ) 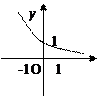




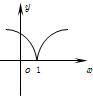
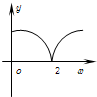








 的反函数是
的反函数是 ,则反函数的解析式是
,则反函数的解析式是 .
. ,则
,则 ________.
________.