题目内容
(本题满分12分)设全集U={2,3,a2+2a-3},A={2,|a+1|},∁UA={5}.
(1) 求a的取值集合D;
(2) 若M={x|x=log2|a|,x∈D},求出集合M的所有子集.
【答案】
(1) D={-4,2}
(2)∅、{1}、{2}、{1,2}
【解析】解:(1)∵A∪(∁UA)=U,………………2分
∴{2,3,a2+2a-3}={2,5,|a+1|},
∴|a+1|=3,且a2+2a-3=5,………………5分
解得a=-4或a=2. ∴ D={-4,2}………………8分
(2) M={log22,log2|-4|}={1,2}.
∴集合M的所有子集为:∅、{1}、{2}、{1,2}…………………12分

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;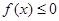 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求