Question

（本小题满分12分）已知数列{an}中，a1＝2，前n项和为Sn，对于任意n≥2，

3Sn－4，an， 总成等差数列．

（I）求数列通项公式an；

（II）若数列满足，求数列的前n项和．

 

Answer 1

【答案】

 

（1）an=2

（2）

【解析】解：（I）∵n≥2时，3Sn－4，an，2－总成等差数列，

∴，

即　，　　                       　…………………………2分　　                   

∴　．

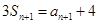两式相减，得?，．…………………………4分

∴a2，a3，…an，…成等比数列．

∵a1=2  当n =2时，a2= ，                 …………………………5分

∴a1，a2，a3，…an，…成等比数列，           …………………………6分

∴an=2．                             …………………………7分

（II）由（I）得 ，

∴　

．                                ………………………9分                 

   ∵ ，               …………………………11分 

   ∴  ．                  …………………………12分