题目内容
在△ABC中,若向量
=(sin2
,1),
=(cos2A+
,4),其中角A,B,C的对边分别是a,b,c,当
∥
时.
(1)求角A的值;
(2)当a=
,S△ABC=
时,求边长b和角B的大小.
| m |
| B+C |
| 2 |
| n |
| 7 |
| 2 |
| m |
| n |
(1)求角A的值;
(2)当a=
| 3 |
| ||
| 2 |
分析:(1)由两个向量共线的性质可得4sin2
=cos2A+
,求出cosA的值,即可得到A的值.
(2)由S△ABC=
求得bc=2,再由余弦定理求得b+c=3,由此求得b、c的值,进而求得角B的值.
| B+C |
| 2 |
| 7 |
| 2 |
(2)由S△ABC=
| ||
| 2 |
解答:解(1)∵
∥
,∴4sin2
=cos2A+
,∴2[1-cos(B+C)]-(2cos2A-1)-
=0,
所以4cos2A-4cosA+1=0,cosA=
,又0<A<π,∴A=
….(6分)
(2)S△ABC=
bcsinA,∴
bc×
=
,∴bc=2.
又a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc=3,
∴(b+c)2=9,b+c=3.
解得
,或
,
当b=2时,求得B=
,当b=1时求得B=
….(12分)
| m |
| n |
| B+C |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
所以4cos2A-4cosA+1=0,cosA=
| 1 |
| 2 |
| π |
| 3 |
(2)S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
又a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc=3,
∴(b+c)2=9,b+c=3.
解得
|
|
当b=2时,求得B=
| π |
| 2 |
| π |
| 6 |
点评:本题主要考查两个向量共线的性质,余弦定理的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目
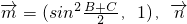 =
= ,4),其中角A,B,C的对边分别是a,b,c,当
,4),其中角A,B,C的对边分别是a,b,c,当 时.
时.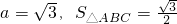 时,求边长b和角B的大小.
时,求边长b和角B的大小.