题目内容
14.联立方程:(1)x-y+3=0,x2+8y2=8
(2)3x-y+2=0,$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1.
分析 (1)(2)利用代入消元法即可得出.
解答 解:(1)由x-y+3=0,可得y=x+3,代入x2+8y2=8,可得x2+8(x+3)2=8,
化为(3x+8)2=0,解得x=-$\frac{8}{3}$,
∴y=3-$\frac{8}{3}$=$\frac{1}{3}$,
∴$\left\{\begin{array}{l}{x=-\frac{8}{3}}\\{y=\frac{1}{3}}\end{array}\right.$;
(2)由3x-y+2=0,可得y=3x+2,代入$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1可得,37x2+48x=0,
解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-\frac{48}{37}}\\{y=-\frac{70}{37}}\end{array}\right.$.
点评 本题考查了方程组的解法“代入消元法”,考查了计算能力,属于基础题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
5.准线方程为x=2的抛物线的标准方程是( )
| A. | y2=-4x | B. | y2=-8x | C. | y2=-x | D. | y2=8x |
6.已知p:x≤1,q:x2-x>0,则p是¬q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
3.如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( )


| A. | 8π | B. | 16π | C. | 32π | D. | 64π |
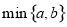 表示
表示 ,
, 两数中的最小值,若函数
两数中的最小值,若函数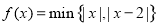 的递增区间为 .
的递增区间为 .