题目内容
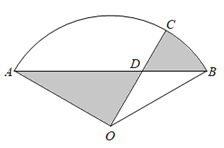
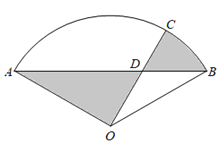
【题目】为响应“生产发展、生活富裕、乡风文明、村容整洁、管理民主”的社会主义新农村建设,某自然村将村边一块废弃的扇形荒地(如图)租给蜂农养蜂、产蜜与售蜜.已知扇形AOB中,![]() ,
,![]() (百米),荒地内规划修建两条直路AB,OC,其中点C在
(百米),荒地内规划修建两条直路AB,OC,其中点C在![]() 上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设
上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设![]() ,蜂巢区的面积为S(平方百米).
,蜂巢区的面积为S(平方百米).
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,蜂巢区的面积S最小,并求此时S的最小值.
为何值时,蜂巢区的面积S最小,并求此时S的最小值.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 等于
等于![]() 时,S取到最小值
时,S取到最小值![]() 平方百米
平方百米
【解析】
(1)由余弦定理得![]() ,由正弦定理得
,由正弦定理得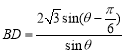 ,
,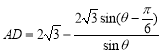 ,蜂巢区的面积
,蜂巢区的面积![]() ,由此能求出
,由此能求出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)对![]() 求导得,当
求导得,当![]() 时,
时,![]() ,
,![]() 递减,当
递减,当![]() 时,
时,![]() ,
,![]() 递增,当
递增,当![]() ,
,![]() 时,
时,![]() ,
,![]() 递减,由此能求出当
递减,由此能求出当![]() 为
为![]() 时,蜂巢区的面积
时,蜂巢区的面积![]() 最小,
最小,![]() 的最小值为
的最小值为![]() .
.
(1)![]() ,
,![]() ,由余弦定理得
,由余弦定理得![]() ,
,
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,![]()
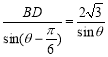 ,
,
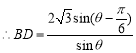 ,
,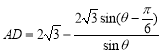 ,
,
![]() 蜂巢区的面积:
蜂巢区的面积:
![]()
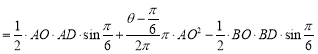 ,
,
整理,得![]() 关于
关于![]() 的函数关系式为:
的函数关系式为:
![]() ,
,![]() .
.
(2)对![]() 求导,得
求导,得![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,![]() 递减,
递减,
当![]() 时,
时,![]() ,
,![]() 递增,
递增,
当![]() ,
,![]() 时,
时,![]() ,
,![]() 递减,
递减,
综上所述,![]() 的最小值只可有在
的最小值只可有在![]() 或
或![]() 趋近
趋近![]() 时取得,
时取得,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 当
当![]() 为
为![]() 时,蜂巢区的面积
时,蜂巢区的面积![]() 最小,
最小,![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目