题目内容
15．某超市五一假期举行促销活动，规定一次购物不超过100元的不给优惠；超过100元而不超过300元时，按该次购物全额9折优惠；超过300元的其中300 元仍按9折优惠，超过部分按8折优惠．（1）写出顾客购物全额与应付金额之间的函数关系，并画出流程图，要求输入购物全额，能输出应付金额．
（2）若某顾客的应付金额为282.8元，请求出他的购物全额．
分析 （1）运用分段函数的形式，顾客购物全额x与应付金额y之间的函数关系，并画出流程图；
（2）由300×0.9=270＜282.2，则该顾客购物全额超过300元，运用第三段函数式，令y=282.8，解出x．
解答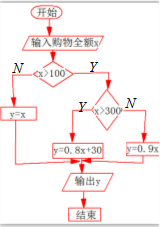 
解：（1）顾客购物全额x与应付金额y之间的函数关系如下
y=$\left\{\begin{array}{l}{x，0＜x≤100}\\{0.9x，100＜x≤300}\\{0.9×300+0.8（x-300），x＞300}\end{array}\right.$，
流程图如右：
（2）设顾客的购物全额为x，则
由300×0.9=270＜282.2，
则该顾客购物全额超过300元，
由y=300×0.9+0.8（x-300）=282.8，
解得x=316，
所以顾客的购物全额为316元．
点评 本题考查分段函数和运用，同时考查流程图的画法，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
1．在区间[0，π]上随机取一个x，sin（x+$\frac{π}{6}$）≥$\frac{1}{2}$的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
10．已知a∈R，若关于x的方程x2+x-|a+$\frac{1}{4}$|+a2=0没有实根，则a的取值范围是（ ）
| A． | （-∞，-1）∪（$\frac{1+\sqrt{3}}{2}$，+∞） | B． | （-∞，$\frac{-1+\sqrt{3}}{2}$）∪（1，+∞） | ||
| C． | （-∞，-1）∪（1，+∞） | D． | （-∞，$\frac{-1-\sqrt{3}}{2}$）∪（$\frac{1+\sqrt{3}}{2}$，+∞） |
20．掷两颗骰子，出现的点数之和是6的概率为（ ）
| A． | $\frac{5}{36}$ | B． | $\frac{1}{12}$ | C． | $\frac{5}{21}$ | D． | $\frac{1}{4}$ |
5．
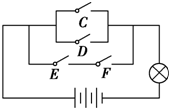一个电路如图所示，C、D、E、F为4个开关，其闭合的概率都是$\frac{1}{2}$，且是相互独立的，则灯亮的概率是（ ）
一个电路如图所示，C、D、E、F为4个开关，其闭合的概率都是$\frac{1}{2}$，且是相互独立的，则灯亮的概率是（ ）| A． | $\frac{9}{16}$ | B． | $\frac{7}{16}$ | C． | $\frac{13}{16}$ | D． | $\frac{3}{16}$ |