题目内容
【题目】设△ABC是边长为4的正三角形,点P1 , P2 , P3 , 四等分线段BC(如图所示) 
(1)P为边BC上一动点,求 ![]()
![]() 的取值范围?
的取值范围?
(2)Q为线段AP1上一点,若 ![]() =m
=m ![]() +
+ ![]()
![]() ,求实数m的值.
,求实数m的值.
【答案】
(1)解:以BC所在直线为x轴,AP2所在直线为y轴,
P2为坐标原点,建立直角坐标系,
则A(0,2 ![]() ),B(﹣2,0),C(2,0),P1(﹣1,0),
),B(﹣2,0),C(2,0),P1(﹣1,0),
设P(t,0)(﹣2≤t≤2),则 ![]() =(﹣t,2
=(﹣t,2 ![]() ),
), ![]() =(2﹣t,0),
=(2﹣t,0),
可得 ![]()
![]() =﹣t(2﹣t)+2
=﹣t(2﹣t)+2 ![]() 0=t2﹣2t=(t﹣1)2﹣1,(﹣2≤t≤2),
0=t2﹣2t=(t﹣1)2﹣1,(﹣2≤t≤2),
t=1时,取得最小值﹣1;t=﹣2时,取得最大值8.
则 ![]()
![]() 的取值范围为[﹣1,8]
的取值范围为[﹣1,8]
(2)解:设Q(x,y),由A,Q,P1共线,
可得 ![]() =
= ![]() ,
,
即有y=2 ![]() x+2
x+2 ![]() ,
,
则 ![]() =(x,2
=(x,2 ![]() x),
x), ![]() =(﹣2,﹣2
=(﹣2,﹣2 ![]() ),
), ![]() =(2,﹣2
=(2,﹣2 ![]() ),
),
若 ![]() =m
=m ![]() +
+ ![]()
![]() ,
,
则 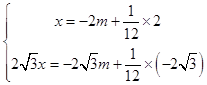 ,
,
解得m= ![]() .
.
【解析】(1)以BC所在直线为x轴,AP2所在直线为y轴,P2为坐标原点,建立直角坐标系,求得A,B,C,P1 , 的坐标,求得向量PA,PC的坐标,运用数量积的坐标表示,再由二次函数在闭区间上的值域求法可得;(2)设Q(x,y),由A,Q,P1共线,运用斜率相等,求得y关于x的式子,再分别求得向量AQ,AB,AC的坐标,得到m,x的方程组,即可解得m的值.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目



