题目内容
求函数y=-2tan(3x+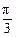 )的定义域、值域,并指出它的周期、奇偶性和单调性
)的定义域、值域,并指出它的周期、奇偶性和单调性
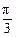 )的定义域、值域,并指出它的周期、奇偶性和单调性
)的定义域、值域,并指出它的周期、奇偶性和单调性所求的函数定义域为{x|x≠ (k∈Z)},值域为R,周期为
(k∈Z)},值域为R,周期为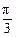 ,它既不是奇函数,也不是偶函数.在区间[
,它既不是奇函数,也不是偶函数.在区间[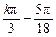 ,
, ](k∈Z)上是单调减函数.
](k∈Z)上是单调减函数.
 (k∈Z)},值域为R,周期为
(k∈Z)},值域为R,周期为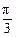 ,它既不是奇函数,也不是偶函数.在区间[
,它既不是奇函数,也不是偶函数.在区间[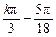 ,
, ](k∈Z)上是单调减函数.
](k∈Z)上是单调减函数.由3x+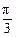 ≠kπ+
≠kπ+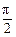 ,得x≠
,得x≠ (k∈Z),
(k∈Z),
∴所求的函数定义域为{x|x≠ (k∈Z)},值域为R,周期为
(k∈Z)},值域为R,周期为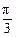 ,
,
它既不是奇函数,也不是偶函数.
kπ-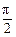 ≤3x+
≤3x+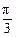 ≤kπ+
≤kπ+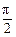 (k∈Z),
(k∈Z),
∴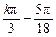 ≤x≤
≤x≤ (k∈Z).
(k∈Z).
在区间[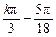 ,
, ](k∈Z)上是单调减函数.
](k∈Z)上是单调减函数.
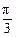 ≠kπ+
≠kπ+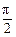 ,得x≠
,得x≠ (k∈Z),
(k∈Z),∴所求的函数定义域为{x|x≠
 (k∈Z)},值域为R,周期为
(k∈Z)},值域为R,周期为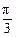 ,
,它既不是奇函数,也不是偶函数.
kπ-
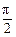 ≤3x+
≤3x+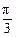 ≤kπ+
≤kπ+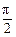 (k∈Z),
(k∈Z),∴
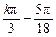 ≤x≤
≤x≤ (k∈Z).
(k∈Z).在区间[
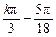 ,
, ](k∈Z)上是单调减函数.
](k∈Z)上是单调减函数.
练习册系列答案
相关题目
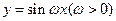 的图象按向量
的图象按向量 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )





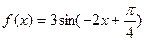 的图像为
的图像为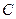 ,下列四个命题正确的是
,下列四个命题正确的是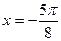 对称 ②
对称 ②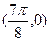
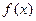 在区间
在区间 是增函数 ④
是增函数 ④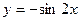 的图像向左平移
的图像向左平移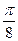 个单位
个单位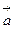 =(1+
=(1+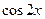 ,1),
,1),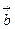 =(1,
=(1,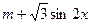 )(
)(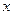 ,
, ∈R),且
∈R),且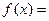
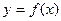 的最小正周期;
的最小正周期;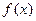 的最大值是4,求
的最大值是4,求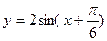 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.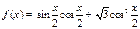 .
.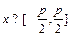 时,求f (
时,求f (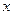 )的值域;
)的值域;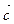 ="(h," k) (0 < h < p)平移,使得平移后的图象关于原点对称,求出向量
="(h," k) (0 < h < p)平移,使得平移后的图象关于原点对称,求出向量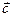 .
. 。
。 时,求函数f(x)的最大值、最小值。
时,求函数f(x)的最大值、最小值。 的部分图象如图所示,则
的部分图象如图所示,则 =( )
=( )



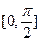 上为减函数的是
上为减函数的是