题目内容
在△ABC中,角A、B、C的对边分别为a、b、c.设 =(bcosC,-1),
=(bcosC,-1), =((c-3a)cosB,1),且
=((c-3a)cosB,1),且 ∥
∥ .
.
(1)求cosB值;
(2)若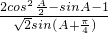 =-
=- 求tanC.
求tanC.
解:(1)∵ ∥
∥ ∴bcosC+(c-3a)cosB=0,(2分)
∴bcosC+(c-3a)cosB=0,(2分)
即sinBcosC+sinCcosB-3sinAcosB=0(3分)
∴sin(B+C)-3sinAcosB=0,又sin(B+C)=sinA
∴sinA(1-3cosB)=0(5分)
∵sinA≠0,∴cosB= ,(6分)
,(6分)
(2)∵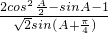 =
=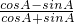 =
=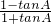 =-
=- (8分)
(8分)
∴tanA=2,tanB=2 (9分)
(9分)
∴tanC=-tan(A+B)=-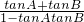 =
=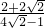 =
=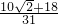 (12分)
(12分)
分析:(1)首先利用向量平行得出bcosC+(c-3a)cosB=0并化简,再根据sin(B+C)=sinA,能够得出sinA(1-3cosB)=0,进而得出cosB= ;
;
(2)利用诱导公式和和差公式化简已知式子,能够得出tanA=2,tanB=2 ,然后由正切的和差公式求出tanC.
,然后由正切的和差公式求出tanC.
点评:本题考查了平行向量的坐标表示以及三角函数的诱导公式和和差公式,解题过程中要灵活运用三角形的内角和等于180°,属于基础题.
 ∥
∥ ∴bcosC+(c-3a)cosB=0,(2分)
∴bcosC+(c-3a)cosB=0,(2分)即sinBcosC+sinCcosB-3sinAcosB=0(3分)
∴sin(B+C)-3sinAcosB=0,又sin(B+C)=sinA
∴sinA(1-3cosB)=0(5分)
∵sinA≠0,∴cosB=
 ,(6分)
,(6分)(2)∵
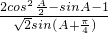 =
=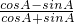 =
=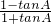 =-
=- (8分)
(8分)∴tanA=2,tanB=2
 (9分)
(9分)∴tanC=-tan(A+B)=-
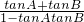 =
=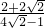 =
=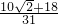 (12分)
(12分)分析:(1)首先利用向量平行得出bcosC+(c-3a)cosB=0并化简,再根据sin(B+C)=sinA,能够得出sinA(1-3cosB)=0,进而得出cosB=
 ;
;(2)利用诱导公式和和差公式化简已知式子,能够得出tanA=2,tanB=2
 ,然后由正切的和差公式求出tanC.
,然后由正切的和差公式求出tanC.点评:本题考查了平行向量的坐标表示以及三角函数的诱导公式和和差公式,解题过程中要灵活运用三角形的内角和等于180°,属于基础题.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |