题目内容
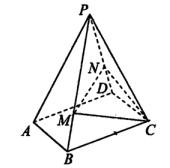
(理)已知直三棱柱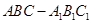 中,
中,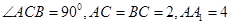 ,
,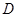 是棱
是棱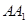 的中点.如图所示.
的中点.如图所示.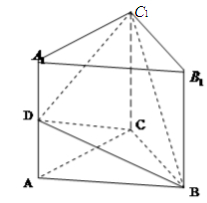
(1)求证: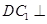 平面
平面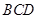 ;
;
(2)求二面角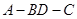 的大小.
的大小.
(1)证明见解析;(2)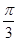 .
.
解析试题分析:(1)本题中由于是直棱柱,且底面中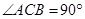 ,即
,即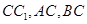 两两垂直,因此我们可以建立空间直角坐标系,用空间向量来解决立体几何问题,要证明线面垂直,只要在平面内任取两个不共线的向量如
两两垂直,因此我们可以建立空间直角坐标系,用空间向量来解决立体几何问题,要证明线面垂直,只要在平面内任取两个不共线的向量如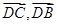 ,只要计算出
,只要计算出 ,
,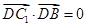 ,就能证明线线垂直,从而得证线面垂直;(2)而要求二面角
,就能证明线线垂直,从而得证线面垂直;(2)而要求二面角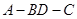 的大小,可通过求两个面
的大小,可通过求两个面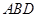 和
和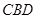 的法向量的夹角来求,法向量的夹角与二面角互补或相等来求,下面就是想办法求法向量了,如平面
的法向量的夹角来求,法向量的夹角与二面角互补或相等来求,下面就是想办法求法向量了,如平面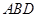 ,可设
,可设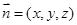 是它的法向量,利用
是它的法向量,利用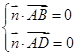 ,得到
,得到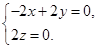 ,只要令
,只要令 ,就可得到一个法向量
,就可得到一个法向量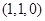 .
.
试题解析:(1)按如图所示建立空间直角坐标系.由题知,可得点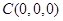 、
、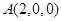 、
、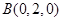 、
、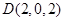 、
、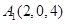 、
、 .
.
于是,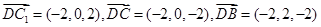 .
.
可算得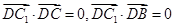 .
.
因此,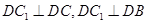 .
.
又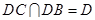 ,
,
所以,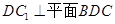 .
.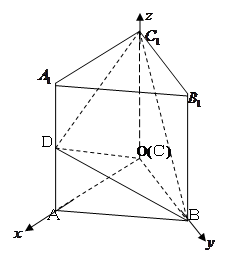
(2)设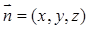 是平面
是平面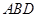 的法向量.
的法向量.
∴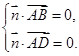
又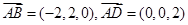 ,
,
∴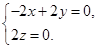 取
取 ,可得
,可得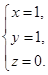 即平面
即平面 的一个法向量是
的一个法向量是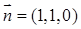 .
.
由(1)知,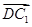 是平面
是平面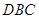 的一个法向量,
的一个法向量,
记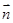 与
与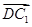 的夹角为
的夹角为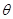 ,则
,则 ,
,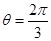 .
.
结合三棱柱可知,二面角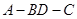 是锐角,
是锐角,
∴所求二面角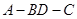 的大小是
的大小是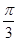 .
.
考点:(1)线面垂直;(2)求二面角.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
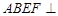 平面
平面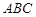 ,四边形
,四边形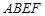 为矩形,
为矩形,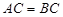 .
. 为
为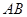 的中点,
的中点,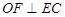 .
.
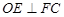 ;
; 时,求二面角
时,求二面角 的余弦值.
的余弦值. ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.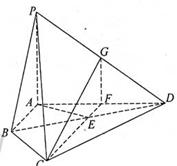
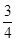 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4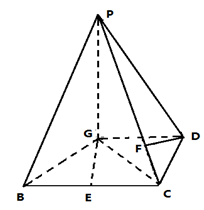
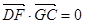 ,
,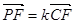 ,求
,求 的值.
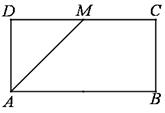
的值. 中,
中,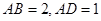 ,
,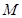 为
为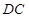 的中点.将
的中点.将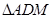 沿
沿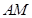 折起,使得平面
折起,使得平面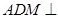 平面
平面 .
.

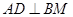 ;
;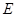 是线段
是线段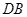 上的一动点,问点E在何位置时,二面角
上的一动点,问点E在何位置时,二面角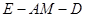 的余弦值为
的余弦值为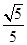 .
.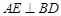 于
于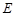 ,延长AE交BC于F,将
,延长AE交BC于F,将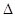 ABD沿BD折起,使平面ABD
ABD沿BD折起,使平面ABD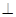 平面BCD,如图2所示.
平面BCD,如图2所示.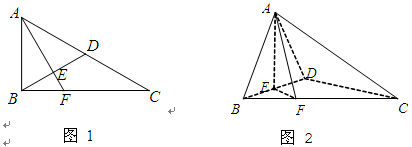
 上是否存在点
上是否存在点 使得
使得 平面
平面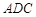 ?若存在,请指明点
?若存在,请指明点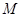 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.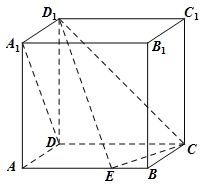
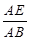 的值;
的值;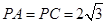 ,
,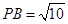 ,M、N两点分别在侧棱PB、PD上,
,M、N两点分别在侧棱PB、PD上,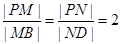 .
.
 ·
· .
.