题目内容
已知椭圆C:| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 3 |
(Ⅰ)求椭圆C和直线l的方程;
(Ⅱ)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若曲线x2-2mx+y2+4y+m2-4=0与D有公共点,试求实数m的最小值.
分析:(Ⅰ)由离心率求得a和b的关系,把点B代入椭圆的方程,联立方程求得a和b,则椭圆的方程可得.
(Ⅱ)把圆的方程整理成标准方程求得圆心和半径,进而利用图象可知只须考虑m<0的情形.设出圆与直线的切点,利用点到直线的距离求得m,进而可求得过点G与直线l垂直的直线的方程,把两直线方程联立求得T,因为区域D内的点的横坐标的最小值与最大值分别为-1,2,所以切点T∉D,由图可知当⊙G过点B时,m取得最小值,利用两点间的距离公式求得m的最小值.
(Ⅱ)把圆的方程整理成标准方程求得圆心和半径,进而利用图象可知只须考虑m<0的情形.设出圆与直线的切点,利用点到直线的距离求得m,进而可求得过点G与直线l垂直的直线的方程,把两直线方程联立求得T,因为区域D内的点的横坐标的最小值与最大值分别为-1,2,所以切点T∉D,由图可知当⊙G过点B时,m取得最小值,利用两点间的距离公式求得m的最小值.
解答: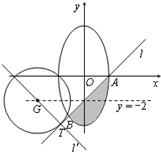 解:(Ⅰ)由离心率e=
解:(Ⅰ)由离心率e=
,得
=
,即a2=3b2.①
又点B(-1,-3)在椭圆C:
+
=1上,即
+
=1.②
解①②得a2=12,b2=4,
故所求椭圆方程为
+
=1.
由A(2,0),B(-1,-3)得直线l的方程为y=x-2.
(Ⅱ)曲线x2-2mx+y2+4y+m2-4=0,
即圆(x-m)2+(y+2)2=8,其圆心坐标为G(m,-2),半径r=2
,
表示圆心在直线y=-2上,半径为2
的动圆.
由于要求实数m的最小值,由图可知,只须考虑m<0的情形.
设⊙G与直线l相切于点T,则由
=2
,得m=±4,
当m=-4时,过点G(-4,-2)与直线l垂直的直线l'的方程为x+y+6=0,
解方程组
,得T(-2,-4).
因为区域D内的点的横坐标的最小值与最大值分别为-1,2,
所以切点T∉D,由图可知当⊙G过点B时,m取得最小值,
即(-1-m)2+(-3+2)2=8,解得mmin=-
-1.
 解:(Ⅰ)由离心率e=
解:(Ⅰ)由离心率e=
| ||
| 3 |
| ||
| a |
| ||
| 3 |
又点B(-1,-3)在椭圆C:
| y2 |
| a2 |
| x2 |
| b2 |
| (-3)2 |
| a2 |
| (-1)2 |
| b2 |
解①②得a2=12,b2=4,
故所求椭圆方程为
| y2 |
| 12 |
| x2 |
| 4 |
由A(2,0),B(-1,-3)得直线l的方程为y=x-2.
(Ⅱ)曲线x2-2mx+y2+4y+m2-4=0,
即圆(x-m)2+(y+2)2=8,其圆心坐标为G(m,-2),半径r=2
| 2 |
表示圆心在直线y=-2上,半径为2
| 2 |
由于要求实数m的最小值,由图可知,只须考虑m<0的情形.
设⊙G与直线l相切于点T,则由
| |m+2-2| | ||
|
| 2 |
当m=-4时,过点G(-4,-2)与直线l垂直的直线l'的方程为x+y+6=0,
解方程组
|
因为区域D内的点的横坐标的最小值与最大值分别为-1,2,
所以切点T∉D,由图可知当⊙G过点B时,m取得最小值,
即(-1-m)2+(-3+2)2=8,解得mmin=-
| 7 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了知识的综合运用和数形结合的方法的应用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C: