题目内容
【题目】已知函数![]() ,
, ![]()
(1)若两函数图象有两个不同的公共点,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,
, ![]() ,求实数
,求实数![]() 的最大值.
的最大值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)由两函数图象有两个不同的公共点可等价于方程![]() 在
在![]() 有两个不同的解,即方程
有两个不同的解,即方程![]() 在
在![]() 有两个不同的解,设
有两个不同的解,设![]() ,求导的函数
,求导的函数![]() 的单调性,从而求出
的单调性,从而求出![]() 的最大值,从而可求出实数
的最大值,从而可求出实数![]() 的取值范围;(2)由
的取值范围;(2)由![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() 对
对![]() 恒成立,设
恒成立,设![]() ,则只需
,则只需![]() ,对
,对![]() 求导分析其单调性,从而可得
求导分析其单调性,从而可得![]() ,即可得到实数
,即可得到实数![]() 的最大值.
的最大值.
试题解析:(1)解:函数![]() 与
与![]() 的图象有两个不同的公共点等价于方程
的图象有两个不同的公共点等价于方程![]() 在
在![]() 有两个不同的解,即方程
有两个不同的解,即方程![]() 在
在![]() 有两个不同的解.
有两个不同的解.
设![]() ,则函数
,则函数![]() 的图象与直线
的图象与直线![]() 有两个不同的交点.
有两个不同的交点.
由![]() ,令
,令![]() ,有
,有![]() .
.
列表如下:
|
|
|
|
| + | 0 | - |
| 增函数 | 极大值 | 减函数 |
∴函数有极大值![]()
∵![]() 时,
时, ![]() ;
; ![]() ,
, ![]()
∴![]()
(注:或①当![]() 时,至多有一个公共点;②当
时,至多有一个公共点;②当![]() 时,因为
时,因为![]() 时,
时, ![]() , 至多有一个公共点;③当
, 至多有一个公共点;③当![]() 时,因为
时,因为![]() ,
, ![]() ,所以
,所以![]() 上有一个零点,又
上有一个零点,又![]() ,而
,而![]() ,所以在
,所以在![]() 上存在一个零点,即
上存在一个零点,即![]() 时,有两个零点)
时,有两个零点)
(2)由题![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,
恒成立,
设![]() ,则只需
,则只需![]() ,由
,由![]() ,
,
又∵![]()
∴![]() 在
在![]() 为增函数
为增函数
∴![]()
又∵![]()
∴存在![]() 使
使![]() ,即
,即![]() ,则
,则![]()
又∵![]() 时,
时, ![]() ,
, ![]() 为减函数,
为减函数, ![]() 时,
时, ![]() ,
, ![]() 为增函数
为增函数
∴
∴![]() 在
在![]() 为增函数
为增函数
∴![]()
![]()
![]()
∴![]() ,故实数
,故实数![]() 的最大值为
的最大值为![]() .
.

【题目】随着科学技术的飞速发展,手机的功能逐渐强大,很大程度上代替了电脑、电视.为了了解某高校学生平均每天使用手机的时间是否与性别有关,某调查小组随机抽取了![]() 名男生、
名男生、![]() 名女生进行为期一周的跟踪调查,调查结果如表所示:
名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机超过 | 平均每天使用手机不超过 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为学生使用手机的时间长短与性别有关?
的前提下认为学生使用手机的时间长短与性别有关?
(2)在这![]() 名女生中,调查小组发现共有
名女生中,调查小组发现共有![]() 人使用国产手机,在这
人使用国产手机,在这![]() 人中,平均每天使用手机不超过
人中,平均每天使用手机不超过![]() 小时的共有
小时的共有![]() 人.从平均每天使用手机超过
人.从平均每天使用手机超过![]() 小时的女生中任意选取
小时的女生中任意选取![]() 人,求这
人,求这![]() 人中使用非国产手机的人数
人中使用非国产手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: 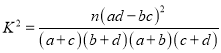
![]()