题目内容
如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
| A.90° | B.60° | C.45° | D.30° |
B
解析试题分析:取AC中点G,连结EG,FG,FG是三角形ABC中位线,GF//AB,GF=AB/2=3,EG是三角形ACD中位线,EG//PC,EG=PC/2=5,故∠EGF是异面直线AB与PC所成角或所成角的补角。
在∆EGF中,根据余弦定理,
cos∠EGF=  ,∠EGF=1200,异面直线AB与PC所成的角为600.
,∠EGF=1200,异面直线AB与PC所成的角为600.
考点:异面直线所成的角;余弦定理。
点评:本题主要考查了空间中异面直线所成的角。求异面直线所成角的步骤:一作二求三说。此题求出∠EGF=1200,但∠EGF并不是异面直线AB与PC所成角,而是所成角的补角。两异面直线所成角的范围为 。
。

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( ) 

A.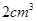 | B. |
C. | D. |
一个棱锥的三视图如图,则该棱锥的表面积(单位:c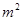 )为( )
)为( )
A.48+12 | B.48+24 | C.36+12 | D.36+24 |
圆锥母线长为1,侧面展开图的圆心角为240°,则圆锥体积为( )
A. | B. | C. | D. |
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列结论中错误的是 ( )
,则下列结论中错误的是 ( )
A. |
B. |
C.三棱锥 的体积为定值 的体积为定值 |
D.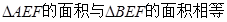 |
若某空间几何体的三视图如图所示,则该几何体的体积是( )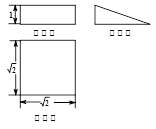
A. | B.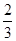 | C.1 | D. 2 |










