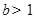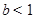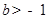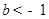题目内容
若将有理数集Q分成两个非空的子集M与N,且满足M∪N=Q,M∩N=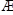 ,M中的每一个元素都小于N中的每一个元素,则称(M,N)为有理数集的一个分割.试判断,对于有理数集的任一分割(M,N) ,下列选项中,不可能成立的是
,M中的每一个元素都小于N中的每一个元素,则称(M,N)为有理数集的一个分割.试判断,对于有理数集的任一分割(M,N) ,下列选项中,不可能成立的是
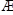 ,M中的每一个元素都小于N中的每一个元素,则称(M,N)为有理数集的一个分割.试判断,对于有理数集的任一分割(M,N) ,下列选项中,不可能成立的是
,M中的每一个元素都小于N中的每一个元素,则称(M,N)为有理数集的一个分割.试判断,对于有理数集的任一分割(M,N) ,下列选项中,不可能成立的是| A.M没有最大元素,N有一个最小元素 | B.M没有最大元素,N也没有最小元素 |
| C.M有一个最大元素,N有一个最小元素 | D.M有一个最大元素,N没有最小元素 |
C
有理数集是无限集合,没有最大值和最小值。而作为有理数集的任一分割(M,N),由于M中的每一个元素都小于N中的每一个元素,则M不存在最小元素(若存在的话,则这个最小元素也是有理数集的最小元素,与有理数集是无限集合矛盾),同理N不存在最大元素,故B成立。
因为 ,所以
,所以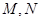 两个必有一个为半开半闭区间一个为开区间,所以M,N不可能同时存在最大元素和最小元素,所以C不成立。
两个必有一个为半开半闭区间一个为开区间,所以M,N不可能同时存在最大元素和最小元素,所以C不成立。
若M为半开半闭区间,N为开区间,则M存在最大元素,而N没有最小元素,此时D成立。
若M为开区间,N为半开半闭区间,则M没有最大元素,而N有最小元素,此时A成立。
综上可得,选C。
因为
 ,所以
,所以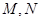 两个必有一个为半开半闭区间一个为开区间,所以M,N不可能同时存在最大元素和最小元素,所以C不成立。
两个必有一个为半开半闭区间一个为开区间,所以M,N不可能同时存在最大元素和最小元素,所以C不成立。若M为半开半闭区间,N为开区间,则M存在最大元素,而N没有最小元素,此时D成立。
若M为开区间,N为半开半闭区间,则M没有最大元素,而N有最小元素,此时A成立。
综上可得,选C。

练习册系列答案
相关题目
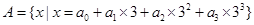 ,其中
,其中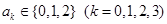 ,且
,且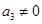 .则
.则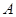 中所有元素之和等于( )
中所有元素之和等于( )
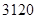
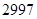
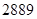
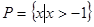 ,那么 ( )
,那么 ( )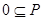
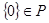
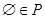
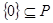
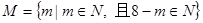 ,则
,则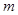 的个数是( )
的个数是( ) 与直线
与直线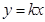 有且仅有两个公共点,则
有且仅有两个公共点,则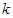 的取值范围是
的取值范围是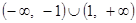
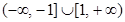

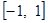
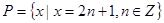 ,
, ,下列结论正确的是( )
,下列结论正确的是( )

 ;
;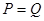 ;
;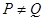 .
.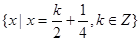 ,N =
,N =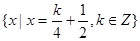 ,则
,则 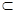 N
N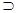 N
N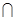 N=
N=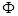
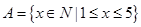 ,则( )
,则( )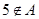


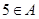
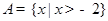 ,
,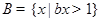 ,其中
,其中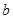 为实数且
为实数且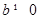 ,则
,则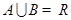 的一个必要不充分条件是( )
的一个必要不充分条件是( )