题目内容
已知函数![]() .
.
(1)当a>0且![]() ,时,试用含a的式子表示b,并讨论f(x)的单调区间;
,时,试用含a的式子表示b,并讨论f(x)的单调区间;
(2)若![]() 有零点,
有零点,![]() ,且对函数定义域内一切满足|x|≥2的实数x有
,且对函数定义域内一切满足|x|≥2的实数x有![]() ≥0.
≥0.
①求f(x)的表达式;
②当x∈(-3,2)时,求函数y=f(x)的图象与函数![]() 的图象的交点坐标.
的图象的交点坐标.
答案:
解析:
解析:
|
解:(1) 由 由 同理 (2)①由(1)及 又由 则 ∴ ②又设 ∵ 故 又 即 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
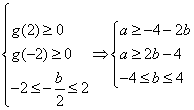 ,结合(i)解得
,结合(i)解得 ,
, 。
。 的单调区间;
的单调区间; 时,
时, 对任意正实数
对任意正实数 都成立;
都成立; ,使得
,使得 对任意的正实数
对任意的正实数 都成立,请直接写出满足这样条件的一个
都成立,请直接写出满足这样条件的一个 。
。 在区间
在区间 上的取值范围;
(2) 当
上的取值范围;
(2) 当 时,
时,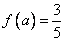 ,求m的值。
,求m的值。