题目内容
已知函数![]() .
.
(1)当![]() =1,求函数
=1,求函数![]() 单调递增区间;
单调递增区间;
(2)当![]() <0且
<0且![]() ∈[0,
∈[0,![]() ]时,函数
]时,函数![]() 的值域为[3,4],求
的值域为[3,4],求![]() +b的值.
+b的值.
解:![]()
=![]() ,
,
(1)当![]() =1时,
=1时,![]() ,
,
∴当![]() 时,
时,
![]() 是增函数,∴
是增函数,∴![]() 的单调递增区间是
的单调递增区间是
[![]() ,
,![]() ](
](![]() ).
).
(2)由![]()
![]() [0,
[0,![]() ]得
]得![]() ≤
≤![]() +
+![]() ≤
≤![]() .
.
∴一![]() ≤sin(
≤sin(![]() +
+![]() )≤1,
)≤1,
∵![]() <0,∴当sin(
<0,∴当sin(![]() +
+![]() )=1时,
)=1时,![]() 取得最小值为3,
取得最小值为3,
当sin(![]() +
+![]() )=-1时,
)=-1时,![]() 取得最大值为4,即
取得最大值为4,即
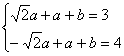 ,解得
,解得![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 。
。 的单调区间;
的单调区间; 时,
时, 对任意正实数
对任意正实数 都成立;
都成立; ,使得
,使得 对任意的正实数
对任意的正实数 都成立,请直接写出满足这样条件的一个
都成立,请直接写出满足这样条件的一个 。
。 在区间
在区间 上的取值范围;
(2) 当
上的取值范围;
(2) 当 时,
时,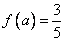 ,求m的值。
,求m的值。