题目内容
(本题14分)已知函数 ,
, 。
。
(1)当t=8时,求函数 的单调区间;
的单调区间;
(2)求证:当 时,
时, 对任意正实数
对任意正实数 都成立;
都成立;
(3)若存在正实数 ,使得
,使得 对任意的正实数
对任意的正实数 都成立,请直接写出满足这样条件的一个
都成立,请直接写出满足这样条件的一个 的值(不必给出求解过程)
的值(不必给出求解过程)
【答案】
(1)函数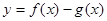 的单调递增区间是
的单调递增区间是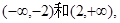 单调递减区间是(-2,2)。
单调递减区间是(-2,2)。
(2)略
(3)存在正实数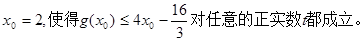
【解析】解:(1)当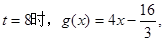
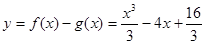
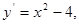
令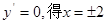 ………………………………………………………………1分
………………………………………………………………1分
令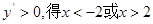
令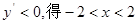 …………………………………………………………3分
…………………………………………………………3分
故所求的函数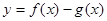 的单调递增区间是
的单调递增区间是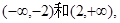 单调递减区间是(-2,2)。…………………………………………………………………………4分
单调递减区间是(-2,2)。…………………………………………………………………………4分
(2)证明:令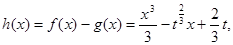
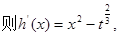
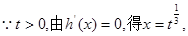 ……………………………………………………6分
……………………………………………………6分
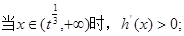
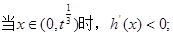 ……………………8分
……………………8分
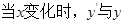 的变化情况如下表
的变化情况如下表
|
|
|
|
|
|
|
_ |
0 |
+ |
|
|
单调递减 |
极小 |
单调递增 |

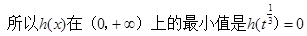
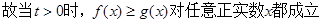 …………………………11分
…………………………11分
(3)存在正实数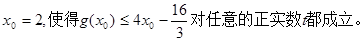 …14分
…14分

练习册系列答案
相关题目
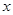
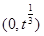
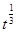
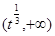
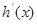
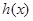
 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。