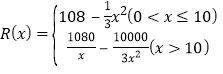Question

【题目】函数的一部分图象如图所示，其中，，.

（1）求函数解析式；

（2）求时，函数的值域；

（3）将函数的图象向右平移个单位长度，得到函数的图象，求函数的单调递减区间.

Answer 1

【答案】（1）；（2）；（3）单调减区间为，.

【解析】

（1）根据最大值和最小值可求，结合周期及特殊点的坐标可求，从而可得解析式；

（2）先根据，求出，结合正弦函数的简图可求的值域；

（3）先根据图象变换求出的解析式，然后可求的单调递减区间.

（1）根据函数的一部分图象，其中，，，

∵，∴；∵，∴，

再根据，可得，，

∴，，∵，∴，

∴函数的解析式为；

（2）∵，∴，∴，

∴函数的值域为；

（3）将函数的图象向右平移个单位长度，

得到函数的图象，

对于函数，

令，，

求得，，

故函数的单调减区间为，.