题目内容
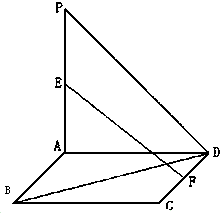 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求EF和平面ABCD所成的角α的正切;
(Ⅲ)求异面直线EF与BD所成的角β的余弦.
分析:(Ⅰ)根据两个平面垂直的性质定理可得 PA⊥平面ABCD.
(Ⅱ)连接AF,则∠AFE即为α.直角三角形EAF中,根据tanα=
运算求得结果.
(Ⅲ)建立空间坐标系,求得得A、B、D、F、E的坐标,可得,
和
的坐标,求得 cosβ=
的值,可得异面直线EF与BD所成的角的余弦值.
(Ⅱ)连接AF,则∠AFE即为α.直角三角形EAF中,根据tanα=
| AE |
| AF |
(Ⅲ)建立空间坐标系,求得得A、B、D、F、E的坐标,可得,
| EF |
| BD |
| ||||
|
|
解答: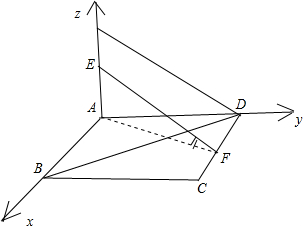 解:(Ⅰ)证明:由于平面PAD⊥平面ABCD,且AD是平面ABCD和平面PAD的交线,
解:(Ⅰ)证明:由于平面PAD⊥平面ABCD,且AD是平面ABCD和平面PAD的交线,
PA在平面PAD内,∠PAD=90°,
根据两个平面垂直的性质定理可得 PA⊥平面ABCD.
(Ⅱ)连接AF,则∠AFE即为α.
直角三角形EAF中,tanα=
=
=
.
(Ⅲ)设正方形的边长为2,以A为原点,以AB所在直线为x轴,以AD所在的直线为y轴,
以AP所在的直线为z轴,建立空间坐标系,
可得A(0,0,0)、B(2,0,0)、D(0,2,0)、F(1,2,0)、E(0,0,1),
∴
=(1,2,-1)、
=(-2,2,0),∴cosβ=
=
=
,
故异面直线EF与BD所成的角的余弦为
.
 解:(Ⅰ)证明:由于平面PAD⊥平面ABCD,且AD是平面ABCD和平面PAD的交线,
解:(Ⅰ)证明:由于平面PAD⊥平面ABCD,且AD是平面ABCD和平面PAD的交线,PA在平面PAD内,∠PAD=90°,
根据两个平面垂直的性质定理可得 PA⊥平面ABCD.
(Ⅱ)连接AF,则∠AFE即为α.
直角三角形EAF中,tanα=
| AE |
| AF |
| ||||
|
| ||
| 5 |
(Ⅲ)设正方形的边长为2,以A为原点,以AB所在直线为x轴,以AD所在的直线为y轴,
以AP所在的直线为z轴,建立空间坐标系,
可得A(0,0,0)、B(2,0,0)、D(0,2,0)、F(1,2,0)、E(0,0,1),
∴
| EF |
| BD |
| ||||
|
|
| -2+4+0 | ||||
|
| ||
| 6 |
故异面直线EF与BD所成的角的余弦为
| ||
| 6 |
点评:本题主要考查直线和平面垂直的判定定理的应用,求直线和平面成的角、异面直线成的角的方法,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.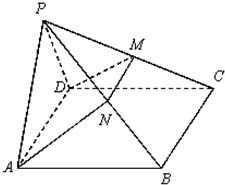 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.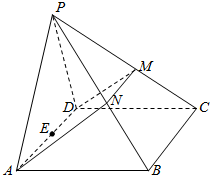 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.