题目内容
(本小题满分12分) 已知函数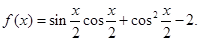
(Ⅰ)将函数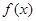 化简成
化简成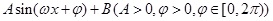 的形式,并指出
的形式,并指出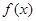 的最小正周期;
的最小正周期;
(Ⅱ)求函数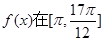 上的最大值和最小值
上的最大值和最小值
【答案】
(Ⅰ)f(x)的最小正周期为2π{k∈Z且k≠0}。
(Ⅱ)f(x)有最小值-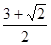 ;f(x)有最大值-2.
;f(x)有最大值-2.
【解析】解 (Ⅰ) f(x)=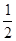 sinx+
sinx+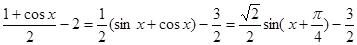 .
.
故f(x)的最小正周期为2π{k∈Z且k≠0}。
(Ⅱ)由π≤x≤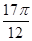 ,得
,得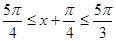 .因为f(x)=
.因为f(x)=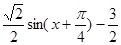 在
在
[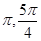 ]上是减函数,在[
]上是减函数,在[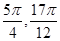 ]上是增函数,故当x=
]上是增函数,故当x=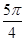 时,f(x)有最小值-
时,f(x)有最小值-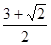 ;而f(π)=-2,f(
;而f(π)=-2,f(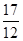 π)=-
π)=-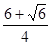 <-2,所以当x=π时,f(x)有最大值-2.
<-2,所以当x=π时,f(x)有最大值-2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目