题目内容
直线A.1个 B.2个 C.3个 D.4个
思路解析:设P1(4cosα,3sinα),a∈(0,![]() ),
),
则![]() =
=![]() =
=![]() ×4sinα+
×4sinα+![]() ×3×4cosα=6(sinα+cosα)=6
×3×4cosα=6(sinα+cosα)=6![]() sin(α+
sin(α+![]() ),
),
当α=![]() 时,
时,![]() 的最大值为6
的最大值为6![]() ,故
,故![]() ≤6
≤6![]() -S△OAB=6
-S△OAB=6![]() -6<3,
-6<3,
故AB的上方不存在满足题意的点P.
又S△OAB=6>3,所以AB的下方在O与AB之间存在2个点满足要求.
答案:B

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 =0,椭圆C:
=0,椭圆C: +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点. +
+ =1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为
=1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为 .
.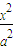 +
+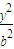 =1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为
=1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为 .
.