题目内容
在三角形ABC中，如果a=2，A=30°，B=120°，则c= ．
分析：由sinA，sinB及a的值，利用正弦定理求出b的值，再由余弦定理列出关系式，将a，b，cosC的值代入计算即可求出c的值．
解答：解：∵a=2，A=30°，B=120°，
∴由正弦定理
=
得：b=
=
=2
，
∵C=180°-30°-120°=30°，
由余弦定理得：c2=a2+b2-2abcosC=4+12-12=4，
则c=2．
故答案为：2
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| asinB |
| sinA |
2×
| ||||
|
| 3 |
∵C=180°-30°-120°=30°，
由余弦定理得：c2=a2+b2-2abcosC=4+12-12=4，
则c=2．
故答案为：2
点评：此题考查了正弦、余弦定理，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
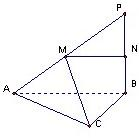如图，在三角形△ABC中，∠ACB=90°，AC=b，BC=a，P是△ABC所在平面外一点，PB⊥AB，M是PA的中点，AB⊥MC，求异面直MC与PB间的距离．
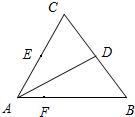如图，在三角形ABC中，D，E分别为BC，AC的中点，F为AB上的点，且
如图：在三角形ABC中，点D为线段AC上的一点，点E为线段BC的中点，连接AE交BD于P点，若
如图，在三角形ABC中，角A，B，C成等差数列，D是BC边的中点，AD=
（2011•崇明县二模）如图，在三角形ABC中，