题目内容
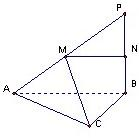 如图,在三角形△ABC中,∠ACB=90°,AC=b,BC=a,P是△ABC所在平面外一点,PB⊥AB,M是PA的中点,AB⊥MC,求异面直MC与PB间的距离.
如图,在三角形△ABC中,∠ACB=90°,AC=b,BC=a,P是△ABC所在平面外一点,PB⊥AB,M是PA的中点,AB⊥MC,求异面直MC与PB间的距离.
分析:作MN∥AB交PB于点N.根据PB⊥AB,AB⊥MC,判断出PB⊥MN,MN⊥MC,判断出MN即为异面直线MC与PB的公垂线段,进而推断出其长度就是MC与PB之间的距离,进而根据勾股定理求得AB,进而求得NM.
解答:解:作MN∥AB交PB于点N.
∵PB⊥AB,∴PB⊥MN.
又AB⊥MC,∴MN⊥MC.
MN即为异面直线MC与PB的公垂线段,
其长度就是MC与PB之间的距离,则得MN=
AB=
.
∵PB⊥AB,∴PB⊥MN.
又AB⊥MC,∴MN⊥MC.
MN即为异面直线MC与PB的公垂线段,
其长度就是MC与PB之间的距离,则得MN=
| 1 |
| 2 |
| 1 |
| 2 |
| a2+b2 |
点评:本题主要考查了点线面间的距离计算.属基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
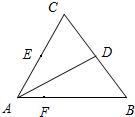 如图,在三角形ABC中,D,E分别为BC,AC的中点,F为AB上的点,且
如图,在三角形ABC中,D,E分别为BC,AC的中点,F为AB上的点,且 (2013•乐山一模)如图,在三角形ABC中,BE是AC边上的中线,O是BE边的中点,若
(2013•乐山一模)如图,在三角形ABC中,BE是AC边上的中线,O是BE边的中点,若 (2011•崇明县二模)如图,在三角形ABC中,
(2011•崇明县二模)如图,在三角形ABC中,