题目内容
 如图,在三角形ABC中,角A,B,C成等差数列,D是BC边的中点,AD=
如图,在三角形ABC中,角A,B,C成等差数列,D是BC边的中点,AD=| 3 |
| 3 |
(1)求边长AC的长;
(2)求sin∠DAC的值.
分析:(I)由A,B,C成等差数列及三角形的内角和定理可求B,然后在△ABD中,由余弦定理可求BD,进而在△ABC中,再次利用余弦定理可求AC
(II)由(I)可得,BD2=AB2+AD2可求∠ABD,∠ADC,在△ADC中,由 正弦定理可得
=
即可求解
(II)由(I)可得,BD2=AB2+AD2可求∠ABD,∠ADC,在△ADC中,由 正弦定理可得
| AC |
| sin∠ADC |
| DC |
| sin∠DAC |
解答:解:(I)∵A,B,C成等差数列
∴A+B+C=3B=π
∴B=
π
在△ABD中,由余弦定理可得AD2=AB2+BD2-2AB•BDcos
π
得3=1+BD2-BD,解得BD=2或BD=-1(舍)
△ABC中,因为BC=2BD=4
所以由余弦定理可得,AC2=AB2+BC2-2AB•BCcos
π
得AC=
(II)由(I)可得,BD2=AB2+AD2
∴∠ABD=
π,∠ADC=
△ADC中,由 正弦定理可得
=
∴sin∠DAC=
sin∠ADC=
∴A+B+C=3B=π
∴B=
| 1 |
| 3 |
在△ABD中,由余弦定理可得AD2=AB2+BD2-2AB•BDcos
| 1 |
| 3 |
得3=1+BD2-BD,解得BD=2或BD=-1(舍)
△ABC中,因为BC=2BD=4
所以由余弦定理可得,AC2=AB2+BC2-2AB•BCcos
| 1 |
| 3 |
得AC=
| 13 |
(II)由(I)可得,BD2=AB2+AD2
∴∠ABD=
| 1 |
| 2 |
| 5π |
| 6 |
△ADC中,由 正弦定理可得
| AC |
| sin∠ADC |
| DC |
| sin∠DAC |
∴sin∠DAC=
| DC |
| AC |
| ||
| 13 |
点评:本题主要考查了等差数列的性质、三角形的内角和定理及正弦定理、余弦定理等知识在求解三角形中的综合应用

练习册系列答案
相关题目
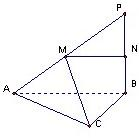 如图,在三角形△ABC中,∠ACB=90°,AC=b,BC=a,P是△ABC所在平面外一点,PB⊥AB,M是PA的中点,AB⊥MC,求异面直MC与PB间的距离.
如图,在三角形△ABC中,∠ACB=90°,AC=b,BC=a,P是△ABC所在平面外一点,PB⊥AB,M是PA的中点,AB⊥MC,求异面直MC与PB间的距离.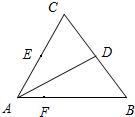 如图,在三角形ABC中,D,E分别为BC,AC的中点,F为AB上的点,且
如图,在三角形ABC中,D,E分别为BC,AC的中点,F为AB上的点,且 (2011•崇明县二模)如图,在三角形ABC中,
(2011•崇明县二模)如图,在三角形ABC中,