题目内容
在直角坐标平面内y轴右侧的一动点P到点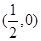 的距离比它到y轴的距离大
的距离比它到y轴的距离大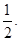
(I)求动点P的轨迹C的方程;
(II)设Q为曲线C上的一个动点,点B,C在y轴上,若△QBC为圆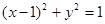 的外切三角形,求△QBC面积的最小值。
的外切三角形,求△QBC面积的最小值。
【答案】
解:(Ⅰ) 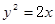 (Ⅱ)
(Ⅱ) 面积的最小值为
面积的最小值为 .
.
【解析】本试题主要是考查了抛物线的方程的求解,以及直线与圆的位置关系,和三角形的面积公式的综合运用。
(1)利用直接法表示出点所满足的几何关系,运用代数的手段表示得到轨迹方程
(2)根据已知条件得到由直线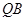 是圆的切线,可知
是圆的切线,可知 ,同理得到
,同理得到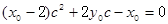 ,然后借助于三角形的面积公式求解最值
,然后借助于三角形的面积公式求解最值
解:(Ⅰ)由题知点 到
到 的距离与它到直线
的距离与它到直线 的距离相等,所以点
的距离相等,所以点 的轨迹是抛物线,方程为
的轨迹是抛物线,方程为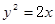 ;……4分
;……4分
(Ⅱ)设 ,则
,则 即
即
由直线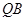 是圆的切线知
是圆的切线知 即
即
同理,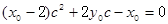 所以
所以 是方程
是方程 的两根
的两根
 ……8分
……8分

又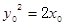
 由题知
由题知
 令
令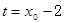 则
则
 当
当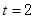 即
即 时,取“
时,取“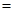 ”
”
 面积的最小值为
面积的最小值为

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
(2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.