题目内容
已知△ABC的周长为6,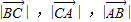 成等比数列,求
成等比数列,求(I)试求∠B的取值范围;
(Ⅱ)求
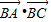 的取值范围.
的取值范围.
【答案】分析:(1)设出三边长,利用△ABC的周长为6,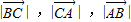 成等比数列,以及余弦定理,求出∠B的取值范围.
成等比数列,以及余弦定理,求出∠B的取值范围.
(2)利用等比数列,求出b的范围,通过向量的数量积,化简为b的表达式,求出数量积的范围即可.
解答:解:(1)设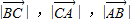 依次为a,b,c
依次为a,b,c
则a+b+c=6,b2=ac,
由余弦定理得cosB=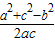
=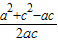
≥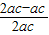 =
=
故有0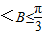 ,…(6分)
,…(6分)
(2)又b=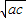 ≤
≤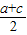 =
=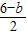 从而0<b≤2
从而0<b≤2
所以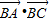 =accosB=
=accosB=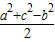
=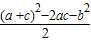
=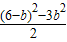
=-(b+3)2+27 …(10分)
∵0<b≤2∴2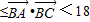 …(12分)
…(12分)
点评:本题考查余弦定理,向量的数量积的应用,考查计算能力,转化思想.
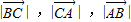 成等比数列,以及余弦定理,求出∠B的取值范围.
成等比数列,以及余弦定理,求出∠B的取值范围.(2)利用等比数列,求出b的范围,通过向量的数量积,化简为b的表达式,求出数量积的范围即可.
解答:解:(1)设
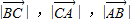 依次为a,b,c
依次为a,b,c则a+b+c=6,b2=ac,
由余弦定理得cosB=
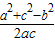
=
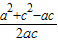
≥
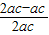 =
=
故有0
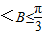 ,…(6分)
,…(6分)(2)又b=
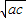 ≤
≤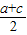 =
=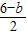 从而0<b≤2
从而0<b≤2所以
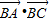 =accosB=
=accosB=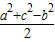
=
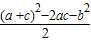
=
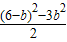
=-(b+3)2+27 …(10分)
∵0<b≤2∴2
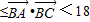 …(12分)
…(12分)点评:本题考查余弦定理,向量的数量积的应用,考查计算能力,转化思想.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目