题目内容
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)在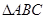 中,若
中,若 的值.
的值.
(1) (2)
(2)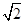
解析试题分析:
(1)要得到 的最小正周期,必须对
的最小正周期,必须对 进行化简,首先观察
进行化简,首先观察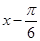 与
与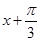 之间的关系,可以发现
之间的关系,可以发现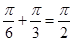 ,故利用诱导公式(奇变偶不变符号看象限)把
,故利用诱导公式(奇变偶不变符号看象限)把
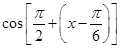 ,再利用正弦的倍角公式即可得到函数
,再利用正弦的倍角公式即可得到函数 的最简形式,利用周期
的最简形式,利用周期 即可得到最小正周期.
即可得到最小正周期.
(2)把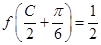 带入(1)得到的
带入(1)得到的 中,化简即可求的C角的大小,A角已知,所以可以求的C,A两个角的正弦值,利用正弦定理可得所求比值即为A,C两个角的正弦之比,带入即可求出
中,化简即可求的C角的大小,A角已知,所以可以求的C,A两个角的正弦值,利用正弦定理可得所求比值即为A,C两个角的正弦之比,带入即可求出 .
.
试题解析:
(1)因为
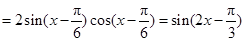 ,
,
所以函数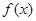 的最小正周期为
的最小正周期为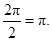 6分
6分
(2)由(1)得,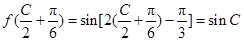 ,
,
由已知, ,又角
,又角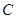 为锐角,所以
为锐角,所以 ,
,
由正弦定理,得 12分
12分
考点:诱导公式正弦定理周期正弦倍角公式

练习册系列答案
相关题目
 内角
内角 所对的边分别是
所对的边分别是 ,且
,且 .
.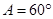 ,求
,求 的值;
的值;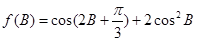 的值域.
的值域.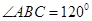 ,
,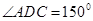 ,
,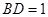 (千米),
(千米),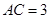 (千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.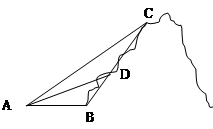
 中,角
中,角 的对边分别为
的对边分别为 .已知
.已知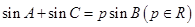 ,且
,且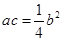 .
. 时,求
时,求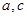 的值;
的值;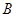 为锐角,求
为锐角,求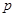 的取值范围.
的取值范围. 中,角
中,角 、
、 、
、 所对的边长分别为
所对的边长分别为 、
、 、
、 ,
,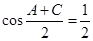 .
.  ,
, ,求
,求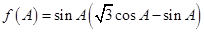 ,求
,求 的取值范围.
的取值范围. 中,
中, 分别是角
分别是角 的对边,且
的对边,且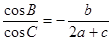 .
.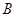 的大小;
的大小;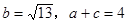 ,求
,求 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 ,
, .
. 的大小;
的大小; ,
, ,求
,求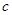 边的长和△
边的长和△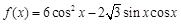 .
. 的最小正周期和值域;
的最小正周期和值域;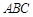 中,角
中,角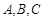 的对边分别为
的对边分别为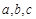 ,若
,若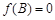 且
且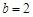 ,
,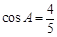 ,求
,求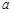 和
和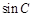 .
.