题目内容
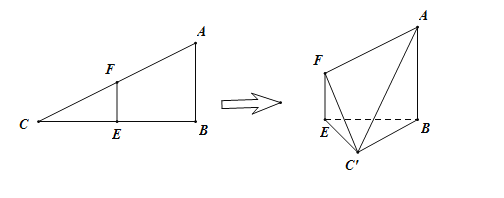
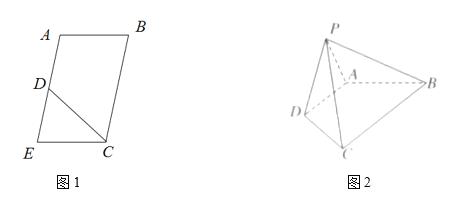
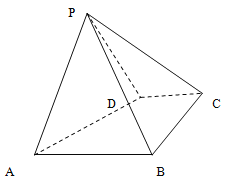
【题目】如图，在四棱锥
中，四边形ABCD为平行四边形，且
，
，
平面PAC.
（1）求证：
平面
；
（2）若异面直线PC与AD所成的角为30°，求二面角
的余弦值.
【答案】（1）证明见解析；（2）
【解析】
（1）根据线面垂直判断定理:如果一条直线垂直一个平面内的两条相交线,那么这条线垂直这个平面，要证
平面
，只需证明
和
，即可求得答案；
（2）先求证
平面
，以A为坐标原点，AB，AC所在直线分别为x，y轴，过点A且与PE平行的直线为z轴，建立空间直角坐标系，求得平面PBC的法向量为
，平面PDC的法向量为
，根据
，即可求得答案.
（1）在
中，
，
，
由余弦定理得：
，
，
，即
平面PAC，
平面PAC，
.
又
平面PAB，
平面PAB，
，
平面PAB.
（2）
，
是异面直线PC与AD所成的角，
又平面
，
，在
中，
，
，
，
，易知
，
在
中，
，
，取AB的中点E，连接PE，则
.
由（1）知平面PAB，
，
又平面，平面ABCD，
，
平面ABCD，
如图，以A为坐标原点，AB，AC所在直线分别为x，y轴，过点A且与PE平行的直线为z轴，建立空间直角坐标系，
则
，
，
，
，
可得：
，
，
，
设平面PBC的法向量为
，
则
取
，则
，
，是平面PBC的一个法向量
设平面PDC的法向量为
，
则
，
则
，取
，则
，
，是平面PDC的一个法向量.
，
由图可知二面角
是钝二面角，
二面角的余弦值为.
名校课堂系列答案
【题目】对于某种类型的口服药，口服
小时后，由消化系统进入血液中药物浓度
（单位）与时间小时的关系为
，其中
，
为常数，对于某一种药物
，
，
．
（1）口服药物后______小时血液中药物浓度最高；
（2）这种药物服药
小时后血液中药物浓度如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0.9545 | 0.9304 | 0.6932 | 0.4680 | 0.3010 | 0.1892 | 0.1163 | 0.072 |
一个病人上午8：00第一次服药，要使得病人血液中药物浓度保持在0.5个单位以上，第三次服药时间是______（时间以整点为准）
【题目】某中学从甲乙两个教师所教班级的学生中随机抽取100人，每人分别对两个教师进行评分，满分均为100分，整理评分数据，将分数以10为组距分成6组：
，
，
，
，
，
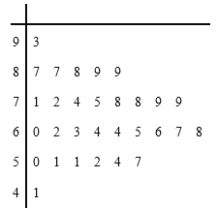
.得到甲教师的频率分布直方图，和乙教师的频数分布表：
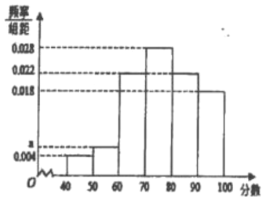
乙教师分数频数分布表 | |
分数区间 | 频数 |
| 3 |
| 3 |
| 15 |
| 19 |
| 35 |
| 25 |
（1）在抽样的100人中，求对甲教师的评分低于70分的人数；
（2）从对乙教师的评分在
范围内的人中随机选出2人，求2人评分均在范围内的概率；
（3）如果该校以学生对老师评分的平均数是否大于80分作为衡量一个教师是否可评为该年度该校优秀教师的标准，则甲、乙两个教师中哪一个可评为年度该校优秀教师？（精确到0.1）
