题目内容
已知集合M={f(x)|f(x)+f(x+2)=f(x+1),x∈R},g(x)=sin(1)判断g(x)与M间的关系,并说明理由;
(2)M中的元素是否都是周期函数,证明你的结论;
(3)M中的元素是否都是奇函数,证明你的结论.
思路分析:f(x)是一个抽象函数,g(x)是一个具体函数,(1)就是让我们判断g(x)是否为f(x)的一个“原函数”,也就是说,g(x)是否满足g(x)+g(x+2)=g(x+1);若g(x)∈M,g(x)为周期函数,其周期为6,那么f(x)也应该是周期函数,其周期也应是6.这就为我们解答(2)指明了方向.
解:(1)∵sin![]() x+sin
x+sin![]() (x+2)
(x+2)
=2sin![]() (x+1)cos
(x+1)cos![]() =sin
=sin![]() (x+1),
(x+1),
即g(x)+g(x+2)=g(x+1),
∴g(x)∈M.
(2)∵f(x)+f(x+2)=f(x+1),
∴f(x+1)+f(x+3)=f(x+2),
由此得出f(x+3)+f(x)=0,
即f(x+3)=-f(x).
∴f(x+6)=-f(x+3)=f(x).
这就表明,f(x)是周期函数,其周期为6.
(3)类似(2),可以证明y=cos![]() x也是M中的元素,但y=cos
x也是M中的元素,但y=cos![]() x不是奇函数.
x不是奇函数.

练习册系列答案
相关题目
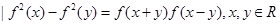 },有下列命题
},有下列命题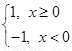 ,则f(x)
,则f(x)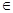 M;
M;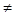 x2),总有
x2),总有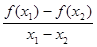 ﹤0成立;
﹤0成立;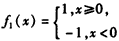 ,则f1(x)∈M;
,则f1(x)∈M;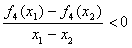 成立;
成立;