��Ŀ����
��f��x��=ex-a��x+1����
��1����a��0��f��x����0��һ��x��R���������a�����ֵ��
��2����g(x)=f(x)+
��A(x1��y1)��B(x2��y2)(x1��x2)������y=g��x�����������㣬���������a��-1��ֱ��AB��б�ʺ���ڳ���m����m��ȡֵ��Χ��
��3���Ƿ����������a��ʹ��1n+3n+��+(2n-1)n��
(an)n��һ��������n�������������ڣ���a����Сֵ���������ڣ���˵�����ɣ�
��1����a��0��f��x����0��һ��x��R���������a�����ֵ��
��2����g(x)=f(x)+
| a |
| ex |
��3���Ƿ����������a��ʹ��1n+3n+��+(2n-1)n��
| ||
| e-1 |
��������1����f��x��=ex-a��x+1����֪f�䣨x��=ex-a����f��x��min=f��lna��=a-a��lna+1��=-alna������f��x����0��һ��x��R���������amax��
��2����f��x��=ex-a��x+1����֪g��x��=f��x��+
=ex+
-ax-a����a��-1��ֱ��AB��б�ʺ���ڳ���m��֪g�䣨x��=ex-
-a��2
-a=-a+2
=m����a��-1�����ɴ������ʵ��m��ȡֵ��Χ��
��3����t��x��=ex-x-1����t�䣨x��=ex-1���Ӷ��õ�ex��x+1��ȡx=-
��i=1��3������2n-1�����ۼӷ��õ�(
)n+(
)n+��+(
)n��e-
+e-
+��+e-
=
��
���ɴ��ܹ��Ƶ�������������a=2��ʹ��1n+3n+��+��2n-1��n��
•��an��n��
��2����f��x��=ex-a��x+1����֪g��x��=f��x��+
| a |
| ex |
| a |
| ex |
| a |
| ex |
ex•(-
|
| -a |
��3����t��x��=ex-x-1����t�䣨x��=ex-1���Ӷ��õ�ex��x+1��ȡx=-
| i |
| 2n |
| 1 |
| 2n |
| 3 |
| 2n |
| 2n-1 |
| 2n |
| 2n-1 |
| 2 |
| 2n-3 |
| 2 |
| 1 |
| 2 |
e-
| ||
| 1-e-1 |
| ||
| e-1 |
| ||
| e-1 |
����⣺��1����f��x��=ex-a��x+1����
��f�䣨x��=ex-a��
��a��0��f�䣨x��=ex-a=0�Ľ�Ϊx=lna��
��f��x��min=f��lna��=a-a��lna+1��=-alna��
��f��x����0��һ��x��R�������
��-alna��0��
��alna��0��
��amax=1��
��2����f��x��=ex-a��x+1����
��g��x��=f��x��+
=ex+
-ax-a��
��a��-1��ֱ��AB��б�ʺ���ڳ���m��
��g�䣨x��=ex-
-a��2
-a=-a+2
=m����a��-1����
���m��3��
��ʵ��m��ȡֵ��Χ�ǣ�-�ޣ�3]��
��3����t��x��=ex-x-1��
��t�䣨x��=ex-1����t�䣨x��=0�ã�x=0��
��x��0ʱt�䣨x����0��f��x���ݼ�����x��0ʱt�䣨x����0��f��x��������
��t��x����СֵΪf��0��=0����ex��x+1��
ȡx=-
��i=1��3������2n-1��
��1-
��e-
����(
)n��e-
��
�ۼӵ�(
)n+(
)n+��+(
)n��e-
+e-
+��+e-
=
��
��
��1n+3n+��+��2n-1��n��
•��2n��n��
�ʴ���������a=2��ʹ��1n+3n+��+��2n-1��n��
•��an��n��
��f�䣨x��=ex-a��
��a��0��f�䣨x��=ex-a=0�Ľ�Ϊx=lna��
��f��x��min=f��lna��=a-a��lna+1��=-alna��
��f��x����0��һ��x��R�������
��-alna��0��
��alna��0��
��amax=1��
��2����f��x��=ex-a��x+1����
��g��x��=f��x��+
| a |
| ex |
| a |
| ex |
��a��-1��ֱ��AB��б�ʺ���ڳ���m��
��g�䣨x��=ex-
| a |
| ex |
ex•(-
|
| -a |
���m��3��
��ʵ��m��ȡֵ��Χ�ǣ�-�ޣ�3]��
��3����t��x��=ex-x-1��
��t�䣨x��=ex-1����t�䣨x��=0�ã�x=0��
��x��0ʱt�䣨x����0��f��x���ݼ�����x��0ʱt�䣨x����0��f��x��������
��t��x����СֵΪf��0��=0����ex��x+1��
ȡx=-
| i |
| 2n |
��1-
| i |
| 2n |
| i |
| 2n |
| 2n-i |
| 2n |
| i |
| 2 |
�ۼӵ�(
| 1 |
| 2n |
| 3 |
| 2n |
| 2n-1 |
| 2n |
| 2n-1 |
| 2 |
| 2n-3 |
| 2 |
| 1 |
| 2 |
e-
| ||
| 1-e-1 |
| ||
| e-1 |
��1n+3n+��+��2n-1��n��
| ||
| e-1 |
�ʴ���������a=2��ʹ��1n+3n+��+��2n-1��n��
| ||
| e-1 |
���������⿼������������ʵ�������ֵ������������������ʵ����ȡֵ��Χ����̽������������ʵ������Сֵ���ۺ���ǿ���Ѷȴ���ʱҪ�������⣬���������㵼�����ʽ��еȼ�ת����

��ϰ��ϵ�д�
 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
�����Ŀ
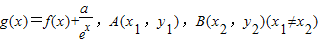 ������y=g��x�����������㣬���������a��-1��ֱ��AB��б�ʺ���ڳ���m����m��ȡֵ��Χ��
������y=g��x�����������㣬���������a��-1��ֱ��AB��б�ʺ���ڳ���m����m��ȡֵ��Χ��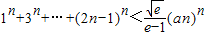 ��һ��������n�������������ڣ���a����Сֵ���������ڣ���˵�����ɣ�
��һ��������n�������������ڣ���a����Сֵ���������ڣ���˵�����ɣ� ������y=g��x�����������㣬���������a��-1��ֱ��AB��б�ʺ���ڳ���m����m��ȡֵ��Χ��
������y=g��x�����������㣬���������a��-1��ֱ��AB��б�ʺ���ڳ���m����m��ȡֵ��Χ��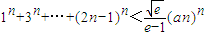 ��һ��������n�������������ڣ���a����Сֵ���������ڣ���˵�����ɣ�
��һ��������n�������������ڣ���a����Сֵ���������ڣ���˵�����ɣ�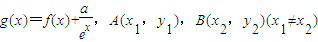 ������y=g��x�����������㣬���������a��-1��ֱ��AB��б�ʺ���ڳ���m����m��ȡֵ��Χ��
������y=g��x�����������㣬���������a��-1��ֱ��AB��б�ʺ���ڳ���m����m��ȡֵ��Χ��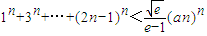 ��һ��������n�������������ڣ���a����Сֵ���������ڣ���˵�����ɣ�
��һ��������n�������������ڣ���a����Сֵ���������ڣ���˵�����ɣ�