题目内容
设f(x)=ex-a(x+1).
(1)若a>0,f(x)≥0对一切x∈R恒成立,求a的最大值.
(2)设g(x)=f(x)+
,且A(x1,y1),B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
(3)求证:1n+3n+…+(2n-1)n<
•(2n)n.
(1)若a>0,f(x)≥0对一切x∈R恒成立,求a的最大值.
(2)设g(x)=f(x)+
| a |
| ex |
(3)求证:1n+3n+…+(2n-1)n<
| ||
| e-1 |
分析:(1)f(x)≥0对一切x∈R恒成立,等价于f(x)min≥0,利用导数可得最小值;
(2)设x1,x2是任意的两实数,且x1g(x1)-mx1,令函数F(x)=g(x)-mx,则F(x)在(-∞,+∞)上单调递增,
F′(x)=g′(x)-m≥0恒成立,分离出参数m后转化为求函数最值即可;
(3)由(1)知ex≥x+1,取x=-
,i=1,3,…,2n-1,得1-
≤e
,即(
)n≤e-
,累加后再进行适当放缩,可证明;
(2)设x1,x2是任意的两实数,且x1g(x1)-mx1,令函数F(x)=g(x)-mx,则F(x)在(-∞,+∞)上单调递增,
F′(x)=g′(x)-m≥0恒成立,分离出参数m后转化为求函数最值即可;
(3)由(1)知ex≥x+1,取x=-
| i |
| 2n |
| i |
| 2n |
| i |
| 2n |
| 2n-i |
| 2n |
| i |
| 2 |
解答:解:(1)∵f(x)=ex-a(x+1),∴f′(x)=ex-a,
∵a>0,f′(x)=ex-a=0的解为x=lna,
∴f(x)min=f(lna)=a-a(lna+1)=-alna,
∵f(x)≥0对一切x∈R恒成立,
∴-alna≥0,∴lna≤0,∴0<a≤1,即amax=1.
(2)设x1,x2是任意的两实数,且x1<x2,
则
>m,故g(x2)-mx2>g(x1)-mx1,
∴不妨令函数F(x)=g(x)-mx,则F(x)在(-∞,+∞)上单调递增,
∴F′(x)=g′(x)-m≥0恒成立,
∴对任意的a≤-1,x∈R,m≤g′(x)恒成立,
g′(x)=ex-a-
≥2
-a=-a+2
=(
+1)2-1≥3,
故m≤3;
(3)由(1)知ex≥x+1,取x=-
,i=1,3,…,2n-1,得1-
≤e
,即(
)n≤e-
,
累加得:(
)n+(
)n+…+(
)n≤e-
+e-
+…+e-
=
<
,
∴1n+3n+…+(2n-1)n<
(2n)n,
故存在正整数a=1.使得1n+3n+…+(2n-1)n<
•(2n)n.
∵a>0,f′(x)=ex-a=0的解为x=lna,
∴f(x)min=f(lna)=a-a(lna+1)=-alna,
∵f(x)≥0对一切x∈R恒成立,
∴-alna≥0,∴lna≤0,∴0<a≤1,即amax=1.
(2)设x1,x2是任意的两实数,且x1<x2,
则
| g(x2)-g(x1) |
| x2-x1 |
∴不妨令函数F(x)=g(x)-mx,则F(x)在(-∞,+∞)上单调递增,
∴F′(x)=g′(x)-m≥0恒成立,
∴对任意的a≤-1,x∈R,m≤g′(x)恒成立,
g′(x)=ex-a-
| a |
| ex |
ex•(-
|
| -a |
| -a |
故m≤3;
(3)由(1)知ex≥x+1,取x=-
| i |
| 2n |
| i |
| 2n |
| i |
| 2n |
| 2n-i |
| 2n |
| i |
| 2 |
累加得:(
| 1 |
| 2n |
| 3 |
| 2n |
| 2n-1 |
| 2n |
| 2n-1 |
| 2 |
| 2n-3 |
| 2 |
| 1 |
| 2 |
e-
| ||
| 1-e-1 |
| ||
| e-1 |
∴1n+3n+…+(2n-1)n<
| ||
| e-1 |
故存在正整数a=1.使得1n+3n+…+(2n-1)n<
| ||
| e-1 |
点评:本题考查恒成立问题、导数求函数的最值,考查转化思想,考查学生分析问题解决问题的能力,该题综合性强,难度大,对能力要求较高.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
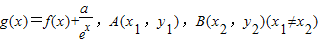 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;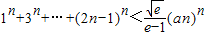 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由. 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;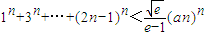 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.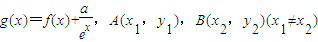 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;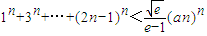 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.