题目内容
(理科)解关于x的不等式:
≥1(a>0)
| x2+a-2 | x+a |
分析:移项整理得
≥0,根据根的大小分类,由穿根法解之即可.
| (x+1)•(x-2) |
| x+a |
解答:解:移项整理得
≥0,
∴①当a>1时,
结合图象得:-a<x≤-1或x≥2;

②当a=1时:x≥2;
≥0等价转化为:x-2≥0,
∴x≥2;
③当0<a<1时,

结合图象得:-1≤x<-a或x≥2.
综上所述:
①当a>1时:解集为:{x|-a<x≤-1或x≥2};
②当a=1时:解集为:{x|x≥2};
③当0<a<1时:解集为:{x|-1≤x<-a或x≥2}.
| (x+1)•(x-2) |
| x+a |
∴①当a>1时,
结合图象得:-a<x≤-1或x≥2;

②当a=1时:x≥2;
| (x+1)•(x-2) |
| x+a |
∴x≥2;
③当0<a<1时,

结合图象得:-1≤x<-a或x≥2.
综上所述:
①当a>1时:解集为:{x|-a<x≤-1或x≥2};
②当a=1时:解集为:{x|x≥2};
③当0<a<1时:解集为:{x|-1≤x<-a或x≥2}.
点评:本题考查了分式不等式的解法,本题关键在于,先移项,后整理,转化为同解的整式不等式,用到穿根法和分类讨论.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
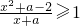 (a>0)
(a>0)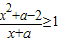 (a>0)
(a>0)